MSE decomposition to Variance and Bias Squared

Question

In showing that MSE can be decomposed into variance plus the square of Bias, the proof in Wikipedia has a step, highlighted in the picture. How does this work? How is the expectation pushed in to the product from the 3rd step to the 4th step? If the two terms are independent, shouldn't the expectation be applied to both the terms? and if they aren't, is this step valid?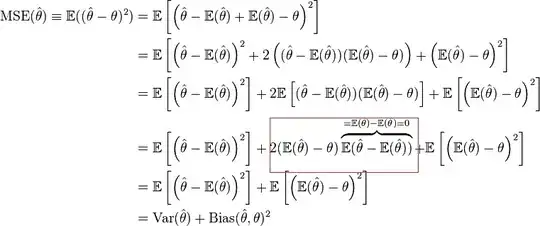 enter image description here

score 29 · Accepted Answer · answered Nov 09 '14 at 19:35

29

The trick is that $\mathbb{E}(\hat{\theta}) - \theta$ is a constant.

answered Nov 09 '14 at 19:35

AdamO

52,330
5
104
209

1

Oh I see. The only unknown here is the estimator. Right? – statBeginner Nov 09 '14 at 19:43
2

Yes. Taking expectation means that the estimator goes to whatever it's estimating, that's what makes the $\mathbf{E}(\hat{\theta} - \mathbf{E}(\hat{\theta}))$ go to 0. – AdamO Nov 09 '14 at 23:38
5

Sorry, that sentence doesn't make much sense to me. If an estimator went to whatever it was estimating, wouldn't that make it unbiased? Can it be explained by saying $\mathbb{E}(\hat{\theta} - \mathbb{E}(\hat{\theta}))$ = $\mathbb{E}(\hat{\theta}) - \mathbb{E}(\mathbb{E}(\hat{\theta}))$ = $\mathbb{E}(\hat{\theta}) - \mathbb{E}(\hat{\theta})$ = 0 ? – user1158559 Apr 06 '17 at 21:16
@user1158559 the product term in the middle is a constant times something with expected value 0. Even if theta-hat is biased, it's still a constant times 0. – AdamO Apr 18 '17 at 15:49
May i know why is E(θ^)−θ a constant? – Bernice Liting Aug 23 '17 at 13:54
@LitingCai both terms are constants: the expectation of a random variable and a parameter do not depend on the data. – AdamO Aug 23 '17 at 16:00
@MartijnWeterings I don't understand. Either $E(\hat{\theta})$ is variable or $\theta$ is variable per your comment. I'll assume non-Bayesian which rules out the latter. You then go on to claim that the *second moment* is non-zero which does *not* mean the variance is non-zero, in fact it is the bias. You then go on to give the mathematical expression of expectation, saying it's constant, which contradicts your earlier argument that $E(\hat{\theta})$ is a variable. – AdamO Sep 21 '17 at 15:23
Adam, you were right (+1), I was confused about the original question, because it mentions *a highlight in the picture* (which is about that term going to zero instead of taking the constant term outside the brackets of the expectation). So I wanted to talk about the variable $\mathbb{E}(\hat{\theta})-\hat{\theta}$, but instead I copied (because I was lazy) from your answer the constant term $\mathbb{E}(\hat{\theta})-\theta$ (and could not change it anymore after 5 minutes). Besides (1) using the wrongly copied term, I also (2) misunderstood the question. The maths used variabl $\hat{\theta}$ – Sextus Empiricus Sep 21 '17 at 16:28
It is constant with respect to expectation, we implicitly assume $\mathbb{E}_\theta[ \mathbb{E}_\theta((\hat{\theta}) - \theta) | \theta]$, another name for the quantity is **risk under the square loss**. Therefore when we take the expectation with respect to $\theta$ the term becomes constant. – Hirak Sarkar Nov 22 '17 at 16:46
Why is it constant? The true label is a function of the random variable $X$ that generates the samples: $\theta=f(X)$, as is the predicted label $\hat{\theta}=g(X)$. How is that constant? Different samples have different true labels. – ngram May 03 '21 at 14:30

Sextus Empiricus · Answer 2 · 2020-05-30T16:47:48.233

There has been some confusion about the question which was ambiguous being about the highlight and the step from line three to line four.

There are two terms that look a lot like each other.

$$\mathbb{E}\left[\hat{\theta}\right] - \theta \quad \text{vs} \quad \mathbb{E}\left[\hat{\theta}\right] - \hat\theta$$

The question, about the step from 3rd to 4th line, relates to the first term:

$\mathbb{E}[\hat{\theta}] - \theta$ this is the bias for the estimator $\hat\theta$

The bias is the same (constant) value every time you take a sample, and because of that you can take it out of the expectation operator (so that is how the step from the 3rd to 4th line, taking the constant out, is done).

Note that you should not interpret this as a Bayesian analysis where $\theta$ is variable. It is a frequentist analysis which conditions on the parameters $\theta$. So we are computing more specifically $\mathbb{E}[(\hat{\theta} - \theta)^2 \vert \theta]$, the expectation value of the squared error conditional on $\theta$, instead of $\mathbb{E}[(\hat{\theta} - \theta)^2]$. This conditioning is often implied implicitly in a frequentist analysis.

The question about the highlighted expression is about the second term

$\mathbb{E}[\hat{\theta}] - \hat{\theta}$ this is the deviation from the mean for the estimator $\hat{\theta}$.

It's expectation value is also called the 1st central moment which is always zero (so that is how the highlighted step, putting the expectation equal to zero, is done).

This is an excellent answer. Thanks. Perhaps this is more trivial, but this question and explanation doesn't seem to explain how one truly gets the 4th expression from the 3rd. To not deviate too much from this particular question, I left a new one [here](https://stats.stackexchange.com/questions/469459/algebra-of-expectations-in-the-mse-decomposition) — Josh, May 30 '20 at 16:40

score 6 · Answer 3 · answered Sep 20 '17 at 23:30

6

$E(\hat{\theta}) - \theta$ is not a constant.

The comment of @user1158559 is actually the correct one:

$$ E[\hat{\theta} - E(\hat{\theta})] = E(\hat{\theta}) - E[E(\hat{\theta})] = E(\hat{\theta}) - E(\hat{\theta}) = 0 $$

answered Sep 20 '17 at 23:30

little_monster

626
6
8

I don't see what you are trying to show. Also the bias may not be zero but that does not mean that it isn't a constant. – Michael R. Chernick Sep 21 '17 at 00:20
It is not a constant because $\hat{\theta} = f(D)$ where $D$ is a given training data, which is also a random variable. Thus, its expectation is not a constant. – little_monster Sep 21 '17 at 00:49
Also, the fact that it is not a constant or not cannot explain how step 4 is possible from step 3. On the other hand, the comment of @ user1158559 explains that. – little_monster Sep 21 '17 at 00:52
@Michael, there has been confusion about the question. The highlighted part contains this expression $\mathbb{E}(\hat{\theta} - \mathbb{E}(\hat{\theta}) )=0$, but in the text of the question it is mentioned that it is instead about the change from the third line to the fourth line, changing the nesting of expectations. – Sextus Empiricus Sep 21 '17 at 15:14
Thanks all - So @SextusEmpiricus based on your above comment, do you agree with this answer that $E(\hat{\theta}) - \theta$ is **not** a constant, or do you still stand with what you wrote in your own answer that $E(\hat{\theta}) - \theta$ is indeed a constant? I mention this because the current accepted and most voted answer say the latter, but this answer dissents with it. – Josh May 30 '20 at 13:56
2

@Josh, yes $$\text{$E(\hat\theta) - \theta$, the bias of the estimator $\hat{\theta}$, is constant}$$ (in the sense that it is the same for each sample). $$\text{$E(\hat\theta) - \hat\theta$, the error of the estimator $\hat\theta$, is not a constant}$$For instance, say we wish to approximate the mean of a normal distributed population by using the median. Then the the bias is $E(\hat\theta) - \theta =0$ and *constantly* the same for every sample, but the estimate $\hat{\theta}$ is not the same for every sample, ie. $E(\hat\theta) - \hat\theta$ will be different each sample. – Sextus Empiricus May 30 '20 at 15:31
Ok thank you - @SextusEmpiricus so to be clear, you are stating that this answer is wrong, right? – Josh May 30 '20 at 15:34
1

@Josh, this answer is *right* about the step in the highlighted block, why the expectation value of the the difference of the estimator with it's expectation value, $E(\hat\theta)-\hat\theta$, which is variable, is zero (note: in the previous comment I wrongly refered to this as the error of the estimator, which is $\hat\theta - \theta$ instead). This answer is wrong about $E(\hat\theta)-\theta$ not being a constant. – Sextus Empiricus May 30 '20 at 15:41
1

Of course, you must not consider this from a Bayesian point of view where $\theta$ is treated as variable, but you must consider it from a frequentist point of view which *conditions* on $\theta$. – Sextus Empiricus May 30 '20 at 15:44

MSE decomposition to Variance and Bias Squared

3 Answers3

Linked