I know there are plenty of questions about the Bias/Variance tradeoff. I've been trying to derive it myself to build some intuition.
I looked at the Wikipedia page, and I saw this: 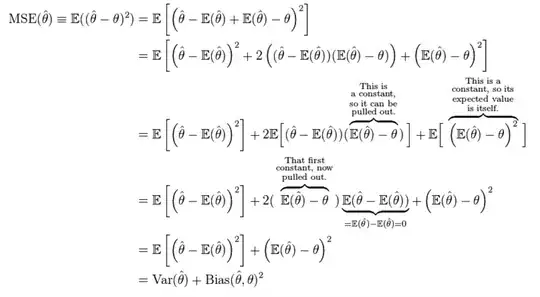
Notice where it says "This is a constant...". Which part of the expression E[theta-hat] - theta is constant?
Let's use linear regression as an example, fitting y=mx+b. After fitting a line, the expected value of y at a given value x is constant, sure, because it is just plugging in x into our linear model. But are we talking about the expected value of our model at a particular x, or the expected value of all of the y's predicted by our model (i.e. the sample mean of the y's, y-bar)?
If it is the latter, then this doesn't seem like a constant value to me. The difference between the true model, and the model estimate will vary depending on x. In linear regression, if the difference didn't vary, then the true linear relationship, and our estimate must be parallel.
What are we calling "constant", e.g. in linear regression? I chose linear regression for its ease of illustrating these concepts.