Testing significance of peaks in spectral density

Question

We sometimes use spectral density plot to analyze periodicity in time series. Normally we analyze the plot by visual inspection and then try to draw a conclusion about the periodicity. But have the statisticians developed any test to check whether any spikes in the plot are statistically different from white noise? Have the R-experts developed any package for spectral density analysis and for doing that kind of test?

Answer 1

You should be aware that estimating power spectra using a periodogram is not recommended, and in fact has been bad practice since ~ 1896. It is an inconsistent estimator for anything less than millions of data samples (and even then ...), and generally biased. The exact same thing applies to using standard estimates of autocorrelations (i.e. Bartlett), as they are Fourier transform pairs. Provided you are using a consistent estimator, there are some options available to you.

The best of these is a multiple window (or taper) estimate of the power spectra. In this case, by using the coefficients of each window at a frequency of interest, you can compute a Harmonic F Statistic against a null hypothesis of white noise. This is an excellent tool for detection of line components in noise, and is highly recommended. It is the default choice in the signal-processing community for detection of periodicities in noise under assumption of stationarity.

You can access both the multitaper method of spectrum estimation and the associated F-test via the multitaper package in R (available via CRAN). The documentation that comes with the package should be enough to get you going; the F-test is a simple option in the function call for spec.mtm.

The original reference that defines both of these techniques and gives the algorithms for them is Spectrum Estimation and Harmonic Analysis, D.J. Thomson, Proceedings of the IEEE, vol. 70, pg. 1055-1096, 1982.

Here is an example using the included data set with the multitaper package.

require(multitaper);
data(willamette);
resSpec <- spec.mtm(willamette, k=10, nw=5.0, nFFT = "default",
                    centreWithSlepians = TRUE, Ftest = TRUE,
                    jackknife = FALSE, maxAdaptiveIterations = 100,
                    plot = TRUE, na.action = na.fail) 

The parameters you should be aware of are k and nw: these are the number of windows (set to 10 above) and the time-bandwidth product (5.0 above). You can easily leave these at these quasi-default values for most applications. The centreWithSlepians command removes a robust estimate of the mean of the time series using a projection onto Slepian windows -- this is also recommended, as leaving the mean in produces a lot of power at the low frequencies.

I would also recommend plotting the spectrum output from 'spec.mtm' on a log scale, as it cleans things up significantly. If you need more information, just post and I'm happy to provide it.

Answer 2

Ronald Fisher proposed an exact test of the maximum periodogram coordinate in R.A. Fisher, Proc. R. Soc A (1929) 125:54. The test is based on the g-statistic. Specifically, the null hypothesis of Gaussian white noise is rejected if g is significantly large, that is, if one of the values ​​of $f(\omega_k)$ is significantly higher than the average of all signals.

You can get more details about the test in MB Priestley, Spectral Analysis and Time Series, Academic Press, London, 1981, page 406.

In R, the package GeneCycle contains the function fisher.g.test():

library(GeneCycle)
?fisher.g.test

Hope this helps.

Answer 3

We have tried an attempt to address this issue by a wavelet transform of a spectral-based test recently in this paper. Essentially, you need to consider the periodogram ordinates distribution, similarly to the article of Fisher, mentioned in the earlier answers. Another paper from Koen is this. We have recently published an R package hwwntest.

Answer 4

Use the spectrum.test function in the ts.extend package

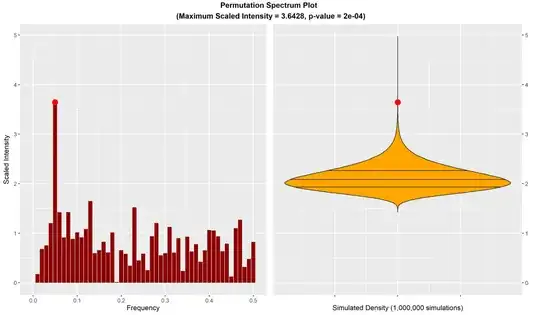
You can conduct a "permutation spectrum test" on your data using the ts.extend package. This is a permutation-based variant of the classic Fisher test that looks at the maximum spectral intensity of the data and compares it to its null distribution under the null hypothesis of exchangeability. (The advantage of this test over the Fisher test is that it does not assume normal error terms in the data; i.e., it works for any underlying distribuiton.) Here is an example where we generate data with a periodic signal and then test for the presence of the signal. The test output and resulting plot easily detects the signal.

#Load the package
library(ts.extend)

#Generate mock data
set.seed(1)
m      <- 100
SIGNAL <- 0.8*sin(0.3*(1:m))
NOISE  <- rnorm(m)
SERIES <- SIGNAL + NOISE

#Conduct permutation-spectrum test
TEST <- spectrum.test(SERIES)
TEST
        Permutation-Spectrum Test

data:  real time-series vector SERIES with 100 values
maximum scaled intensity = 3.6428, p-value = 0.000208
alternative hypothesis: distribution of time-series vector is not exchangeable 
(at least one periodic signal is present)

#Plot the test results
plot(TEST)