1

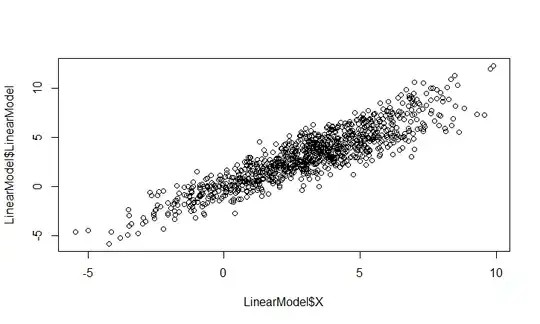
Plot of Linear Data

Plot of Residual values of Linear Model

Probability density function of residuals

Above are three plots of the Linear model I am trying to analyze. The first one is a basic plot of the linear data:

LinearModel = read.csv(file= "C:/Users/Nikhil/Documents/LinearModelCase2.csv", 
                       header=TRUE, sep=",")
plot(LinearModel$X,LinearModel$LinearModel)

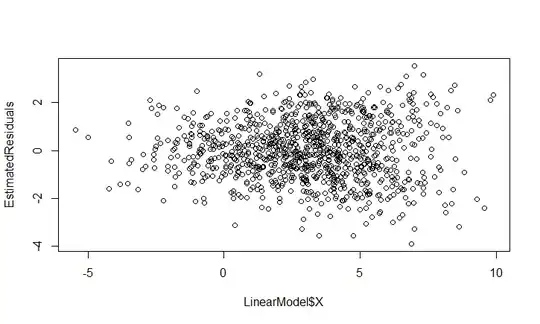
The second one is plot of the residuals (error values) based on the estimated linear model using the given data:

EstimatedLinearModel <- lm(LinearModel$LinearModel~LinearModel$X)
EstimatedResiduals   <- EstimatedLinearModel$residuals
plot(LinearModel$X,EstimatedResiduals)

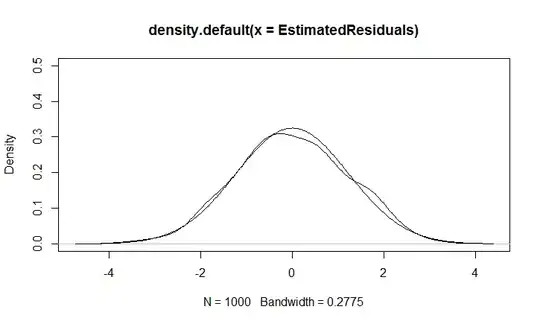
The third is a plot of the probability density function of the residuals using this code:

Probability.Density.Residuals <- density(EstimatedResiduals)
plot(Probability.Density.Residuals, ylim=c(0,.5))
lines(Probability.Density.Residuals$x, 
  dnorm(Probability.Density.Residuals$x, mean=mean(EstimatedResiduals), 
            sd=sd(EstimatedResiduals)))

To me the linear model looks like a mix of two or more different linear models. If this is the case how do I go about separating the two or more linear models using R?

Please let me know if this question does not make any sense, I am new to R and statistics.

gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
Nikhil Agrawal
  • 11
  • 2
  • 2
    I don't see 2 different models lurking in your data. Can you clarify what you are referring to / why you think so? (I do see heteroscedasticity.) Please don't sign your posts or add 'thanks'. If you are just asking for code, this question would be off-topic here (but note the [flexmix](http://cran.r-project.org/web/packages/flexmix/index.html) package may be what you want). – gung - Reinstate Monica Oct 21 '14 at 17:18
  • What are your grounds for identifying a mix? Examples that good for linear regression belong in a textbook. – Nick Cox Oct 21 '14 at 17:18
  • I was looking for a way that I could make the probability density function of the residuals not look wavy and skewed like it does in this picture. What is the indicator of heteroscedasticity? – Nikhil Agrawal Oct 21 '14 at 17:22
  • I was thinking this data is a mix because in the first graph with the linear model, the data seems to be spreading further out as it moves along the x axis. My initial thought was that there are two models in this data with two different slopes. Does that make any sense? – Nikhil Agrawal Oct 21 '14 at 17:23
  • It's presumably what @gung was calling heteroscedasticity. It might indicate that you can better with a transformation. Perhaps another predictor is lurking somewhere. – Nick Cox Oct 21 '14 at 21:39
  • What you are talking about ("spreading further...") is evidence that the variance of the errors is not constant, not evidence of mixture of 2 models. To understand heteroscedasticity, it may help you to read my answer here: [What does having "constant variance" in a linear regression model mean?](http://stats.stackexchange.com/a/52107/7290) – gung - Reinstate Monica Oct 21 '14 at 21:46
  • I see the mixture, too. It might or might not be real ("significant"), but one approach you can take is detailed at http://stats.stackexchange.com/questions/60394/separate-time-series-data-into-two-trends. A closely related approach is called [switching regression](http://support.sas.com/documentation/cdl/en/etsug/63348/HTML/default/viewer.htm#etsug_model_sect094.htm). – whuber Oct 21 '14 at 22:44

0 Answers0