Proper normalized cross-correlation

Question

I'm confused with the widely used approach to compute the normalized cross-correlation which is something like this:

1. Standardize the argument vectors (of equal length $n$).
2. Slide one over the other computing the dot-product of the intersection (correct at least for real vectors).
3. Optionally, define 95% confidence interval as $\pm\frac{2}{\sqrt{n}}$.

Autocorrelation of $\mathcal{N}(0,1)$ sample by this method looks like this:

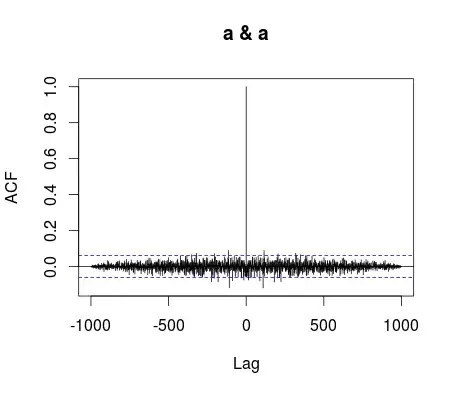
I can achieve such a result using xcorr_common function from this gist:

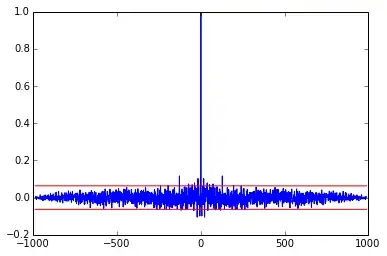
But it seems to me that this method is pretty confusing, because the arguments are standardized in total and not for each intersection. Moreover, the confidence interval derived from the total arguments length is incorrect for the lesser intersections.

I think, the correct (or at least a not-less-correct) result should look like this:

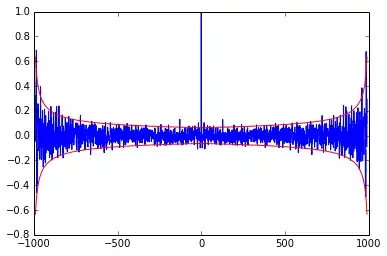
This example is generated using xcorr function from the gist.

The confidence interval here is computed as $\pm\frac{2}{\sqrt{n-k}}$, where $k$ is the lag and $n-k$ is the available intersection length. Each intersection is standardized independently.

After this introduction I can ask my question: am I deadly wrong with this strange "proper" approach or am I inventing a wheel? :) Is it safe to work with cross-correlation calculated by the latter approach? Is it really more "proper" than the commonly used approach? If so, why even R uses the former method?

Thanks in advance.

* For basic info on confidence intervals for cross-correlation refer to:

1. Stats StackExchange answer by Rob Hyndman: https://stats.stackexchange.com/a/3128/43304
2. Guidelines for testing the autocorrelation or cross correlation

---

As it's pointed by whuber in his comment, this question is closely related to a number of already existing ones:

• Understanding this acf output
• Formula for autocorrelation in R vs. Excel

...and probably others with pretty good answers.