3

Animal model (frequently used in animal science and sometime in human or plants) is mixed model with:

$y$ = $X$$b$ + $Z$$u$ + $e$

y is observed values for any quantitative variable, $Xb$ is fixed effects terms while $Zu$ is random effects, and $e$ is residual. Covariance between terms of $u$ can be defined as: $G$ = $A$$\sigma$$^2$$u$ . $A$ is additive relationship matrix whereas $\sigma$$^2$$u$ is additive genetic variance. $A$ can estimated from pedigree or from markers most commonly as $M$$M'$ where $M$ is marker scores (-1,0,1) x observation matrix.

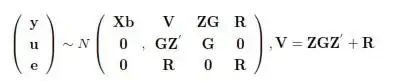
enter image description here

If there are no fixed effects in the model above model can be re-written as:

$y$ = $Z$$u$ + $e$

As $A$ is estimated from large number of markers with multi-colinarity it is logical to shrink the $u$ toward 0 using ridge shrinkage. From the above information we can calculate Best Linear Predictors (BLUPs).

enter image description here

Here for individual i, the BLUP estimate is $yi$, which is summation of $ai$ is additive genetic effect and $ei$ is residual.

Is there any R software package that can do this ? Examples appreciated.

John
  • 2,088
  • 6
  • 27
  • 37

2 Answers2

2

The mixed.solve or kin.blup functions from R package rrBLUP can do the type of analysis you are talking. In addition to reference manual in CRAN, the official website consists of vignettes. Here is an example from the package:

require(rrBLUP)

#random population of 200 individuals/lines with 1000 markers
M <- matrix(rep(0,200*1000),200,1000)
for (i in 1:200) {
  M[i,] <- ifelse(runif(1000)<0.5,-1,1)
}

#random phenotypes
u <- rnorm(1000)
g <- as.vector(crossprod(t(M),u))
h2 <- 0.5  #heritability
y <- g + rnorm(200,mean=0,sd=sqrt((1-h2)/h2*var(g)))


#predict breeding values, here we are using MM' as relatedness measure 
# using function A.mat 
ans <- mixed.solve(y,K=A.mat(M), method="REML", bounds=c(1e-09, 1e+09))
# y is vector of y observations, K is kinship or relatedness matrix
# the defualt method is REML, the bounds specifies the upper and lower bound for 
# ridge parameter 

# BLUP estimation 
ans$u 

# if you are interested in prediction marker effects 
ans <- mixed.solve(y,Z=M)  #By default K = I

# MM' matrix, measure of relatedness, use function A.mat  
A <- A.mat(M)

# The kin.blup is wrapper function for mixed.solve, can also be used.
rdorlearn
  • 3,493
  • 6
  • 26
  • 29
0

You can also try the sommer package (>=3.7) which allows you to put as many random effects as needed, as many covariance structures as needed, and as many responses as well.

For example, the GBLUP model can be fitted as:

data(DT_cpdata)
#### create the variance-covariance matrix
A <- A.mat(GT) # additive relationship matrix
#### look at the data and fit the model
head(DT)
mix.gblup <- mmer(Yield~1,
              random=~vs(id,Gu=A)
                      + Rowf + Colf,
              rcov=~units,
              data=DT)
summary(mix.gblup)

here not only the genetic term but also other random effects are used. The rrBLUP model can be fitted as:

mix.rrblup <- mmer(Yield~1,
              random=~vs(GT)
                      + Rowf + Colf,
              rcov=~units,
              data=DT)
summary(mix.rrblup)
Covaruber
  • 21
  • 2