4

There are well-known HOV tests, for example Levene's, Brown-Forsythe's, Bartlett's available in SAS and R.

But $C_v$ also deals with dispersion, can we use it to understand the degree of HOV?

July 15, 2014 UPDATE:

For example, if

$C_{v_1}$ > $C_{v_2}$,

where $C_{v_1}$ is the coefficient of variation for sample 1 and $C_{v_2}$ is the coefficient of variation for sample 2, can we say that the assume that samples 1 and 2 are differently dispersed?

P.S. by "dispersion" I mean variance (standard deviation).

Nick Cox
  • 48,377
  • 8
  • 110
  • 156
abc
  • 1,747
  • 3
  • 17
  • 32
  • 1
    You can have constant coefficient of variation while variance changes. You can even have constant variance while coefficient of variation changes. So looking at (say) Levene's test won't directly tell you about coefficient of variation. Are you asking instead whether those tests might be modified to deal with comparisons of coefficient of variation? – Glen_b Jul 13 '14 at 20:48
  • @Glen_b: you answered my q in your first two clauses... Thank you – abc Jul 15 '14 at 03:02
  • I can give an answer that gives examples of the first two statements, if you like. ... and addresses the edit, specifically. – Glen_b Jul 15 '14 at 03:04

2 Answers2

3

The coefficient of variation is the standard deviation divided by the mean.

But Cv also deals with dispersion, can we use it to understand the degree of HOV?

If by dispersion, you mean 'standard deviation' or 'variance', then not unless you fix the mean at a constant: then changes is coefficient of variation would reflect changes in spread (and so changes in variance).

Consider:

  1. You can have constant coefficient of variation while variance changes.

    Consider a family of random variables with gamma distributions with fixed shape parameter, $\alpha=\alpha_0$ but varying scale parameter, $\beta$.

    Since the coefficient of variation is only a function of $\alpha$, it will be constant, while the variance ($=\alpha\beta$) changes as $\beta$ changes.

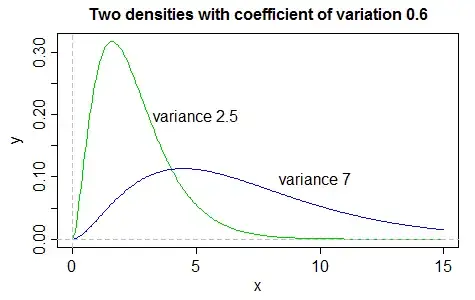
enter image description here

  1. You can even have constant variance while coefficient of variation changes.

    Consider another gamma family, this time with $\alpha$ varying and with $\beta=k/\alpha$ for some constant $k$. Then the variance of every member of the family is $k$, while the coefficient of variation is different for each different $\alpha$.

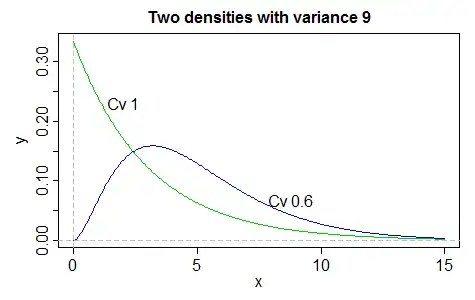
enter image description here

So looking at (say) Levene's test won't directly tell you about coefficient of variation and differences in coefficient of variation won't tell you directly about variance. In either case, you can only tell by bringing the mean (or something that determines the mean given the other information) into it.

For example, if

$C_{v_1} > C_{v_2}$

where $C_{v_1}$ is the coefficient of variation for sample 1 and $C_{v_2}$ is the coefficient of variation for sample 2, can we say that the assume that samples 1 and 2 are differently dispersed?

Again, it depends on what you mean by 'dispersion'. As indicated in case 2. above, they might have identical spread and still differ in coefficient of variation, so if you mean 'different standard deviation' (or different variance), then no.

If instead you define 'dispersion' in terms of CV, then clearly you can say that, yes.

Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • 1
    By the way: _Limpert et al._ [indicate](http://bioscience.oxfordjournals.org/content/51/5/341.full) CV as a measure of dispersion ([table 1](http://bioscience.oxfordjournals.org/content/51/5/341/F1.expansion.html)) – abc Aug 06 '14 at 17:46
  • 2
    stan - Yes, different people use the term differently - some use it to mean spread, others CV, and likely still others something else - hence my caution near the start of my post where I say "If by dispersion you mean...". Thanks for the link; it's good to have examples. – Glen_b Aug 06 '14 at 22:52
1

Homogeneity of variance usually means that the variance do not depend on the mean. To test it, then you need at least two groups, with different means. The coefficient of variation (Cv) is the standard deviation divided by the mean, it usually only makes sense when all means are positive (and it is a unit-free measure). For instance, with Poisson (count data) the variance is equal to the mean, so the coefficient of variation will be $\sigma/\mu = \mu^{1/2}/\mu = \mu^{-1/2}$. For exponentially distributed data, the coefficient of variation is exactly equal to one. In this way, a plot of the coefficient of variation versus the mean may be informative about possible data models.

But it cannot be used to indicate HOV, as usually defined.

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467