MLE2 (in R): I can't find the right starting values

Question

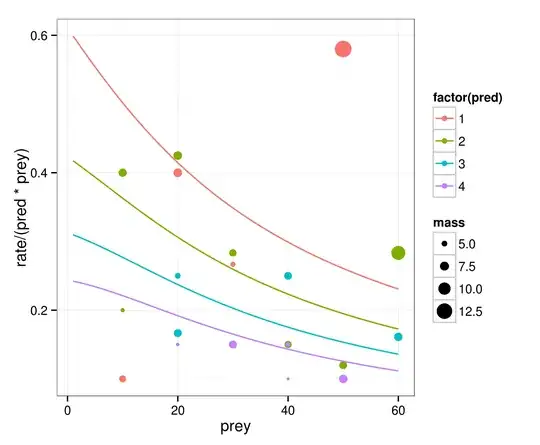
I am trying to fit several MLEs on a small dataset. I have managed to get it done for all my potential models except for this last one. This last one is actually the model that I expected to be the best model, because it was the best model when I did the whole thing using GLS. To start, here is the data:

dat$rate <- c(8,1,17,34,8,30,8,15,17,4,29,12,29,12,12,18,24,20,10,2,4)
dat$pred <- c(2,1,2,2,1,3,1,3,2,1,1,2,3,2,4,4,4,4,3,1,2)
dat$prey <- c(10,10,20,60,20,40,30,20,30,40,50,40,60,50,20,30,40,50,20,10,10)
dat$mass <- c(6.885000,5.942000,7.199000,11.285500,7.263000,6.571667,  4.583000,4.949000,6.220000,2.730000,13.330000,6.074000,7.053667,6.626000, 3.291500,6.711750,4.530750,7.076750,6.644333,2.861000,3.793500)

Here is the function that contains the equation:

CM = function(N0,a,h,tt,P,m, S, al) {
a = a/(1+m*(P-1)+a*h*m*(P-1)*N0)
h=h*S^al
N0 - lambertW(a*h*N0*exp(-a*(P*tt-h*N0)))/(a*h)
}

And here the model:

model = function(eaten, initial, attack, handling, time.exp, pred.no, interf, mass, allometric) {
if (attack < 0 || handling < 0) return(NA)
prop.exp = CM(N0=initial, a = attack, h = handling, tt = time.exp, P = pred.no, m=interf, S= mass, al= allometric)/initial
likelihoods = dbinom(eaten, prob = prop.exp, size = initial, log = TRUE)
negLL = -sum(likelihoods)
return(negLL)
}

And finally the code to fit the model

cm3 = mle2(model,
       start = list(attack = .02, handling = .02, interf=0.02, allometric = -0.2),
       data = list(initial = dat$prey,
                       eaten = dat$rate,
                   pred.no = dat$pred,
                       mass = dat$mass
       ),
       fixed = list(time.exp = 1)
)

I have tried many different starting values and they all ended up with error messages like:

 non-finite finite-difference value [2]

or

 initial value in 'vmmin' is not finite

I guess that either "attack" or "handling" returns an invalid value but I am not sure how to fix this. Any ideas or suggestion are really appreciated.

Thanks in advanced, Robbie

Answer 1

Data:

 dat <- data.frame(rate=c(8,1,17,34,8,30,8,15,17,4,29,12,29,12,12,18,24,20,10,2,4),
              pred=c(2,1,2,2,1,3,1,3,2,1,1,2,3,2,4,4,4,4,3,1,2),
              prey=c(10,10,20,60,20,40,30,20,30,40,50,40,60,50,20,30,
              40,50,20,10,10),
              mass=c(6.885,5.942,7.199,11.2855,
              7.263,6.571667,  4.583,4.949,6.22,2.73,
              13.33,6.074,7.053667,6.626,
              3.2915,6.71175,4.53075,7.07675,6.644333,2.861,3.793500))

CM <- function(N0,a,h,tt,P,m, S, al) {
    a <- a/(1+m*(P-1)+a*h*m*(P-1)*N0)
    h <- h*S^al
   N0 - lambertW(a*h*N0*exp(-a*(P*tt-h*N0)))/(a*h)
}

Is there a mistake here? does unscaled h apply to the last expression but not to the calculation of a ? In general it's a bit dangerous to replace variables in this way (e.g. it might be better to use a2, h2 to clarify that these are new/rescaled variables ...

model <- function(eaten, initial, attack, handling,
                  time.exp=1, pred.no, interf, mass, allometric) {
    if (attack < 0 || handling < 0) return(NA)
    prop.exp <- CM(N0=initial, a = attack, h = handling, tt = time.exp,
                   P = pred.no, m=interf, S= mass, al= allometric)/initial
    likelihoods <- dbinom(eaten, prob = prop.exp, size = initial, log = TRUE)
    negLL = -sum(likelihoods)
    return(negLL)
}

library(plyr) ## for rename()
library(emdbook) ## for lambertW

Set up initial parameters:

spar <- list(attack = .02, handling = .02, interf=0.02, allometric = -0.2)

Version of data with names suitable for model:

dat2 <- rename(dat,
               c(rate="eaten",
                 prey="initial",
                 pred="pred.no"))

Check initial value gives reasonable answer:

do.call(model,c(spar,as.list(dat2)))

I came up with this after a few iterations -- used options(error=recover) to figure out what the bad parameters are, and realized that several parameters shouldn't be allowed to be zero (it also helps to keep the lower bounds just a little bit away from zero, and to set the parameter scales to the same order of magnitude as the results -- this is of course a bit recursive, although you may have a good idea of the orders of magnitude in advance; I detected further problems when trying to run the high-resolution profile below ...).

library(bbmle)
cm3 <- mle2(model,
            start = spar, data = dat2,
            method="L-BFGS-B",lower=c(rep(0.001,3),-Inf),
            control=list(parscale=c(1,2.5,0.01,2)))

pp <- profile(cm3)
png("prof1.png")
plot(pp,show.points=TRUE)
dev.off()

Confidence intervals:

confint(pp)
##                   2.5 %     97.5 %
## attack      0.607584374  1.6905882
## handling             NA 10.7060242
## interf      0.002015405  0.0271424
## allometric -3.305619184 -1.4366461

The allometric parameter profile is a bit wonky, retry it at higher resolution.

pp2 <- profile(cm3,std.err=rep(0.01,4),
   maxsteps=1000,which="allometric")
png("prof2.png")
plot(pp2,show.points=TRUE)
dev.off()

confint(pp2)
##     2.5 %    97.5 % 
## -3.301826 -1.802605 

I'm not exactly sure why this parameter is problematic -- would have to look more closely.

Plot predicted values:

preddat <- expand.grid(N0=1:60,P=1:4)
preddat$S <- mean(dat$mass)
spar3 <- as.list(c(tt=1,rename(coef(cm3),c(attack="a",
             handling="h",allometric="al",interf="m"))))
preddat$rate <- apply(preddat,1,function(x) do.call(CM,c(as.list(x),spar3)))
library(ggplot2)
theme_set(theme_bw())
ggplot(dat,aes(prey,rate/(pred*prey),colour=factor(pred)))+
    geom_point(aes(size=mass))+
    geom_line(data=rename(preddat,c(N0="prey",P="pred")))
ggsave("predplot.png")