strucchange package on ARIMA model

Question

Is there a way to use strucchange package in R on ARIMA models? I haven't been able to find any. Thanks a lot.

Answer 1

The package strucchange requires as input the formula of a linear model to be passed to lm. I don't think there is a straightforward way to use the package with function arima. I don't know either any other R packages implementing this but I can give some basic guidelines that may be helpful for your purposes.

You can carry out some diagnostics based on the cumulative sum of squared residuals (CUMSUM) and based on F-tests for the parameters of the model in different subsamples.

Let's take for illustration the following simulated AR process, x. The first 50 observations are generated from an AR(1) model and the next 100 observations from an AR(2) model:

set.seed(135)
x1 <- arima.sim(model = list(order = c(1,0,0), ar = -0.2), n = 50)
x2 <- arima.sim(model = list(order = c(2,0,0), ar = c(0.3, 0.5)), n = 100)
x <- ts(c(x1, x2))

CUMSUM approach: Once an AR model is fitted to the entire series the CUMSUM process can be obtained as follows:

fit <- arima(x, order = c(2,0,0), include.mean = FALSE)
e <- residuals(fit)
sigma <- sqrt(fit$sigma2)
n <- length(x)
cs <- cumsum(e) / sigma

As a reference, confidence limits can be obtained as done in package strucchange for the OLS-based CUSUM test. For that, we can create an object of class efp and plot it:

require(strucchange)
retval <- list()
retval$coefficients <- coef(fit)
retval$sigma <- sigma
retval$process <- cs
retval$type.name <- "OLS-based CUSUM test"
retval$lim.process <- "Brownian bridge"
retval$datatsp <- tsp(x)
class(retval) <- c("efp")
plot(retval)

The confidence limits are just for reference, I'm not sure they are the right values to carry out a formal test in this context. Regardless of this, a sudden change or shift in the sequence cs can be interpreted as a sign that something is going on around that time point, possibly a structural change. In the plot we observe that at around observation 50, where we introduced a change in the data generating process.

F-tests: Another approach is based on F-test statistics computed as: $$ Fstat = \frac{RSS - USS}{RSS/n} $$ where RSS is the residual sum of squares in the restricted model (the model fitted for the entire data) and USS is the residual sum of squares of models fitted to two subsamples. The statistics can be computed iteratively for the following sequence of subsamples: from observations 1 to 20 and 21 to $n$; then from 1 to 21 and a next subsample from 22 to $n$, and so on as done below:

rss <- sum(residuals(fit)^2)
sigma2 <- fit$sigma2
stats <- rep(NA, n)
for (i in seq.int(20, n-20))
{
  fit1 <- arima(x[seq(1,i)], order = c(2,0,0), include.mean = FALSE)
  fit2 <- arima(x[seq(i+1,n)], order = c(2,0,0), include.mean = FALSE)
  ess <- sum(c(residuals(fit1), residuals(fit2))^2)
  stats[i] <- (rss - ess)/sigma2
}

Similarly to the CUMSUM plot, a plot of the F-statistics may reveal the presence of a structural change. A 95% confidence limit can be obtained based on the chi-square distribution.

plot(stats)
abline(h = qchisq(0.05, df = length(coef(fit)), lower.tail = FALSE), lty = 2, col = "red")

If the minimum p-value related to each statistic is below a significance level, e.g. 0.05, then we can suspect that there is a structural change at that point. In this simulated series that happens at observation 50, when the AR coefficients changed in the data generating process:

which.min(1 - pchisq(stats, df = 2))
#[1] 50

You may find further details in the vignette of the strucchange package that you probably already know and in the references therein.

Answer 2

I have blogged about detecting structural break using the strucchange package in R. It is pretty straight forward - here's the outline:

# assuming you have a 'ts' object in R 

# 1. install package 'strucchange'
# 2. Then write down this code:

library(strucchange)

# store the breakdates
bp_ts <- breakpoints(ts)

# this will give you the break dates and their confidence intervals
summary(bp_ts) 

# store the confidence intervals
ci_ts <- confint(bp_ts)

## to plot the breakpoints with confidence intervals
plot(ts)
lines(bp_ts)
lines(ci_ts)

The time series data used in my blog happens to be an ARIMA(0,1,1) process. If you want to verify that, check my Github repo regarding the same.

Answer 3

If you want to check the existence of structure breaks, I would recommend you to:

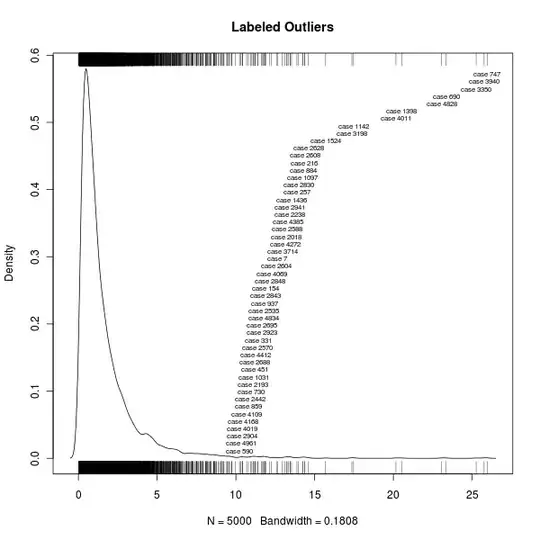
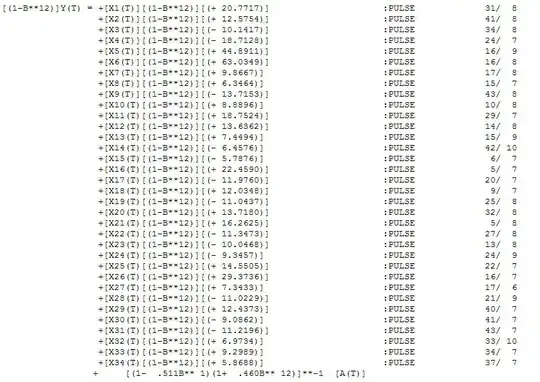
1. Make outliers analysis, with the package tsoutliers. By using the function tso, you can check if your model has an isolated spike (additive outlier), an abrupt change in the mean level (level shift), a spike that takes a few periods to disappear (transient change) or a shock in the innovations of the model (intervention outlier).

2. Analyse the stability of parameters through the QLR test (see critical values in Andrews, 2006). This test is most appropriate when: i) the break date is unknown, ii) the lagged variable is an explanatory variable e/or iii) the errors are heteroscedatic / autocorrelated.

To run this test, you have to add dummies to your model and make loop, in which regressions are calculated several times and the value of the dummies is changed over the time in order to capture possible breaks.

#Define the window to be tested. In general, the first and last 15% observations are excluded
window_breaks <- seq(inic_anomes, last_anomes, 1/12)

# Loop to run the regressions and compute the test statistic
for(i in 1:length(window_breaks)) {

  # Set up dummy variable
  D <- time(y) > window_breaks[i]

  # Estimate model with dummy
  model <- lm(y ~ x + D + D*x)

  # Compute and save the F-statistic
  Fstats[i] <- linearHypothesis(model,
                                c("D", "x:D"),
                                vcov = kernHAC)$F[2]
}

QLR <- max(Fstats) #if QLR < critical value, there is no break