1

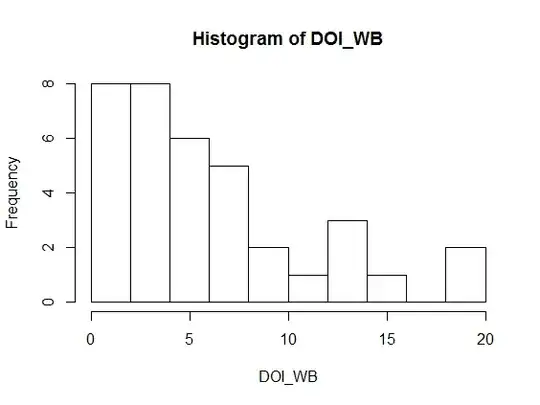
My question is very similar to this previous post. I'm searching for the right distribution family to use in a GAM. My data are disease occurrence on benthic organisms (continuous response variable) and are right skewed (see histogram below). I would like to test the relationship between disease occurrence and percentage cover (continuous covariable) including the effect of Site (fixed categorical) and Zone (random, nested within Site).

I don't have many zeros, and these are true zeros, therefore I don't think a zero-inflated model would be the most appropriate. So my question is: which would be the most appropriate distribution family to use? Any advice would be highly appreciated, thanks!

enter image description here

Community
  • 1
GQU
  • 41
  • 1
  • 6
  • Can you describe your data in a bit more detail? Are they disease counts at independent locations (often Poisson-distributed), or some measure of disease severity of a single organism (perhaps Gamma-distributed)? – P Schnell Jun 20 '14 at 11:41
  • Hi-The factor Site has 6 levels and 6 transects were conducted at each Site. For each transect we counted the number of lesions and the % cover of algae present. Disease occurrence was calculated by dividing the number of lesions by the coverage (number of lesions per m2) therefore they are not disease counts but continuous. This is why I excluded a Poisson distribution. Also I have a few true zeros therefore Gamma distribution won't work as well I guess. Hope that answers your question. Let me know if you need more details. – GQU Jun 20 '14 at 12:43
  • Well, actually, the data *do* have Poisson distributions: the key is to analyze the counts themselves and incorporate the coverage as an "offset" in the analysis. – whuber Jun 20 '14 at 13:55
  • @whuber Hi-Just to be sure I have it right: by "adding the coverage as an offset" do you mean using the coverage as a covariable along with Site and Zone and using the number of lesions as the response variable? – GQU Jun 20 '14 at 14:14
  • An offset enters the model in a slightly different way than the independent variables do. For a general account of offsets, please see the Wikipedia article on [Poisson regression](http://en.wikipedia.org/wiki/Poisson_regression#.22Exposure.22_and_offset), and for more discussions, examples, and working code see [our thread on using offsets](http://stats.stackexchange.com/questions/25415). Note that they can apply to count models generally, not just to Poisson responses. – whuber Jun 20 '14 at 15:09
  • @whuber Great, thanks a lot, I did not know about offset. I will look into it. Is it possible to incorporate an offset in GAMM as well? – GQU Jun 20 '14 at 15:23
  • @whuber Hi-I have been reading a lot about offsets and it is not clear to me how I should use it in my model (GAMM). I am interested in determining if there is a relationship between the number of counts and the coverage. If I add coverage as an offset (separate parameter, not in the formula) then the output won't tell me if there is or not a relationship. I have the feeling I should add it in the formula but did not find the right way to do it. Hope you can help so I can follow your suggestion. – GQU Jun 22 '14 at 07:53
  • In principle you should be able to use % cover both as an offset and an explanatory variable for the counts. If your software will not permit that, then at least for a GLM with log link you can just drop the offset term and correct the estimated coefficients by adding $1$ to the coverage coefficient. – whuber Jun 22 '14 at 14:25

0 Answers0