Constructing a discrete r.v. having as support all the rationals in $[0,1]$

Question

This is the constructivist sequel of this question.

If we can't have a discrete uniform random variable having as support all the rationals in the interval $[0,1]$, then the next best thing is:

Construct a random variable $Q$ that has this support, $Q\in \mathbb{Q}\cap[0,1]$, and that it follows some distribution. And the craftsman in me requires that this random variable is constructed from existing distributions, rather than created by abstractly defining what we desire to obtain.

So I came up with the following:

Let $X$ be a discrete random variable following the Geometric Distribution-Variant II with parameter $0<p<1$, namely

$$ X \in \{0,1,2,...\},\;\;\;\; P(X=k) = (1-p)^kp,\;\;\; F_X(X) = 1-(1-p)^{k+1}$$

Let also $Y$ be a discrete random variable following the Geometric Distribution-Variant I with identical parameter $p$, namely

$$ Y \in \{1,2,...\},\;\;\;\; P(Y=k) = (1-p)^{k-1}p,\;\;\; F_Y(Y) = 1-(1-p)^k$$

$X$ and $Y$ are independent. Define now the random variable

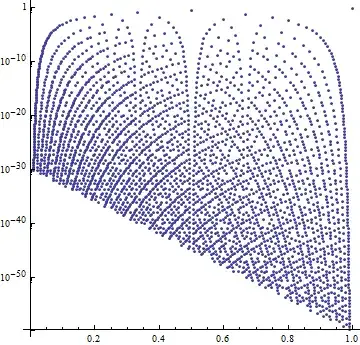
$$Q = \frac {X}{Y}$$

and consider the conditional distribution

$$P(Q\leq q \mid \{X\leq Y\})$$

In loose words "conditional $Q$ is the ratio of $X$ over $Y$ conditional on $X$ being smaller or equal than $Y$." The support of this conditional distribution is $\{0,1,1/2,1/3,...,1/k,1/(k+1),...,2/3,2/4,...\} = \mathbb{Q}\cap[0,1]$.

The "question" is: Can somebody please provide the associated conditional probability mass function?

A comment asked "should it be closed-form"? Since what constitutes a closed-form nowadays is not so clear cut, let me put it this way: we are searching for a functional form into which we can input a rational number from $[0,1]$, and obtain the probability (for some specified value of the parameter $p$ of course), leading to an indicative graph of the pmf. And then vary $p$ to see how the graph changes.

If it helps, then we can make the one or both bounds of the support open, although these variants will deprive us of the ability to definitely graph the upper and/or lower values of the pmf. Also, if we make open the upper bound, then we should consider the conditioning event $\{X<Y\}$.

Alternatively, I welcome also other r.v.'s that have this support(s), as long as they come together with their pmf.

I used the Geometric distribution because it has readily available two variants with the one not including zero in the support (so that division by zero is avoided). Obviously, one can use other discrete r.v.'s, using some truncation.

I most certainly will put a bounty on this question, but the system does not immediately permit this.

Answer 1

Consider the discrete distribution $F$ with support on the set $\{(p,q)\,|\, q \ge p \ge 1\}\subset \mathbb{N}^2$ with probability masses

$$F(p,q) = \frac{3}{2^{1+p+q}}.$$

This is easily summed (all series involved are geometric) to demonstrate it really is a distribution (the total probability is unity).

For any nonzero rational number $x$ let $a/b=x$ be its representation in lowest terms: that is, $b\gt 0$ and $\gcd(a,b)=1$.

$F$ induces a discrete distribution $G$ on $[0,1]\cap \mathbb{Q}$ via the rules

$$G(x) = G\left(\frac{a}{b}\right) = \sum_{n=1}^\infty F\left(an, bn\right)=\frac{3}{2^{1+a+b}-2}.$$

(and $G(0)=0$). Every rational number in $(0,1]$ has nonzero probability. (If you must include $0$ among the values with positive probability, just take some of the probability away from another number--like $1$--and assign it to $0$.)

To understand this construction, look at this depiction of $F$:

$F$ gives probability masses at all points $p,q$ with positive integral coordinates. Values of $F$ are represented by the colored areas of circular symbols. The lines have slopes $p/q$ for all possible combinations of coordinates $p$ and $q$ appearing in the plot. They are colored in the same way the circular symbols are: according to their slopes. Thus, slope (which clearly ranges from $0$ through $1$) and color correspond to the argument of $G$ and the values of $G$ are obtained by summing the areas of all circles lying on each line. For instance, $G(1)$ is obtained by summing the areas of all the (red) circles along the main diagonal of slope $1$, given by $F(1,1)+F(2,2)+F(3,3)+\cdots$ = $3/8 + 3/32 + 3/128 + \cdots = 1/2$.

This figure shows an approximation to $G$ achieved by limiting $q\le 100$: it plots its values at $3044$ rational numbers ranging from $1/100$ through $1$. The largest probability masses are $\frac{1}{2},\frac{3}{14},\frac{1}{10},\frac{3}{62},\frac{3}{62},\frac{1}{42},\ldots$.

Here is the full CDF of $G$ (accurate to the resolution of the image). The six numbers just listed give the sizes of the visible jumps, but every part of the CDF consists of jumps, without exception:

Answer 2

I'll put my comments together and post them as an answer just for clarity. I expect you won't be very satisfied, however, as all I do is reduce your problem to another problem.

My notation:

$Q$ is a RV whose support is $\mathbb{Q}\cap\left[0,1\right]$ -- my $Q$ is not the same as the $Q$ the OP constructs from his $\frac{X}{Y}$. We'll define this $Q$ using $Y$ and $f$, which I introduce below.

$Y$ is any RV whose support is $\mathbb{N}\equiv\left\{1, 2, \ldots\right\}$ -- the $Y$ given by the OP would work, for example.

$f$ is any one-to-one correspondence $f:\mathbb{N}\rightarrow\mathbb{Q}\cap\left[0,1\right]$ and $f^{-1}$ is its inverse. We know these exist.

Now I claim I can reduce your problem to just finding an $f$ and its $f^{-1}$:

Just let $Q=f\left(Y\right)$ and you are done. The PMF of $Q$ is $\Pr[Q =q] = \Pr[Y = f^{-1}(q)]$.

Edit:

Here is a function g that plays the role of $f$, despite not being a one-to-one correspondence (because of duplicates):

g <- function(y) {
    y <- as.integer(y)
    stopifnot(y >= 1)
    b <- 0
    a <- 0
    for (unused_index in seq(1, y)) {
        if (a >= b) {
            b <- b+1
            a <- 0
        } else {
            a <- a+1
        }
    }
    return(sprintf("q = %s / %s", a, b))
    ## return(a / b)
}

Answer 3

One obvious way to construct discrete distributions on the set $\mathbb{Q}_* \equiv \mathbb{Q} \cap [0,1]$ is to do so via sequences of values on that set that cover that set. Suppose you have some arbitrary surjective function $H: \mathbb{N} \rightarrow \mathbb{Q}_*$, which can be interpreted as a sequence on $\mathbb{Q}_*$ that fully covers $\mathbb{Q}_*$ (due to the fact it is surjective). Then you can form a distribution with support $\mathbb{Q}_*$ by taking any probability distribution with support $\mathbb{N}$ and then transforming over to $\mathbb{Q}_*$ using the mapping/sequence $H$.

To see exactly how this is done, let's suppose we have a distribution with support on the natural numbers with the probability mass function $g$. Let $\mathcal{N}_q \equiv \{ n \in \mathbb{N} | h(n)=q \}$ denote the preimage for the rational number $q \in \mathbb{Q}_*$. We can then obtain a probability mass function on the support $\mathbb{Q}_*$ by taking:

$$f(q) = \sum_{n \in \mathcal{N}_q} g(n) \quad \quad \quad \text{for all } q \in \mathbb{Q}_*.$$

There are lots of well-known surjective functions from the natural numbers to various subsets of the rational numbers, and these can easily be used to obtain a mapping/sequence $H$ of the above type. This will always give a valid probability distribution on the desired set, but it won't always be possible to write the probability mass function in a simple form. In general, if you can write the set $\mathcal{N}_q$ in a simple way then you will be able to write the probability mass $f$ in a simple way.

---

Example (Construction using the Calkin-Wilf tree): Consider the Calkin-Wilf sequence which is defined recursively by:

$$\bar{H}(n+1) = \frac{1}{\lfloor \bar{H}(n) \rfloor - \bar{H}(n)+1} \quad \quad \quad \bar{H}(1) = 1.$$

This is a surjective function that maps the natural numbers onto the set of all positive rational numbers. We can obtain a surjective mapping $H: \mathbb{N} \rightarrow \mathbb{Q}_*$ from this sequence by taking:

$$H(n+1) = \min \bigg( \bar{H}(n), \frac{1}{\bar{H}(n)} \bigg). \quad \quad \quad H(1) = 0.$$

The sequence $\bar{H}$ involves a quasi-symmetry property where rational numbers and their inverses appear in a regular pattern. This allows you to simplify the above form using the $\text{fusc}$ function, giving the alternative form:

$$H(n+1) = \frac{\min(\text{fusc}(n), \text{fusc}(n+1))}{\max(\text{fusc}(n), \text{fusc}(n+1))}.$$

The sequence $H$ runs through all the numbers in $\mathbb{Q}_*$ twice, except for zero and one, which each appear only once (as the first two elements of the sequence).