5

I was reading online, and I found that

If the Variance of X increases then the value of R-squared increases

If the Variance of the residuals increases then the value of R-squared decreases

Can someone explain the intuition behind these two statements.

I am generally confused about the impact of variance of X or the residuals on the explanatory power of the regression.

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
LSE123
  • 123
  • 1
  • 5
  • Especially if it's online, you should link to your source for context. – Gregor Thomas May 21 '14 at 17:36
  • It's a general question on the impact of new regressors on R-squared. The website didn't give an example. – LSE123 May 21 '14 at 18:05
  • 1
    The relationship between $R^2$ and the spread of the independent variables ($X$) is discussed and illustrated at http://stats.stackexchange.com/questions/13314. The relationship with the residuals is obvious once you recognize that $1-R^2$ is directly related to the variance of the residuals. – whuber May 21 '14 at 19:25

1 Answers1

4

It's best to think in terms of ratios, how much error is explained by $x$, how much is residual.

If we think of a super-simple regression with one independent variable and slope = 1, just $y = x + \epsilon$, then $\mathrm{Var}(Y) =\mathrm{Var}(X) + \mathrm{Var}(\epsilon)$. (Of course, using the assumption that the residual error $\epsilon$ is uncorrelated with $X$.) From that, it's straightforward that as the variance of $X$ increases, so does the variance of $Y$--if you observe a wider range of $X$ values, you'll also observe a wider range of $Y$ values.

However, we assume that the residual error is fixed, it doesn't change with $X$. And we know that R^2 is defined as the ratio of "explained variance" to "total variance". So

$$ R^2 = \frac{\mathrm{Var}(X)}{\mathrm{Var}(Y)} = \frac{\mathrm{Var}(X)}{\mathrm{Var}(X) + \mathrm{Var}(\epsilon)} $$

And it's pretty clear that, given a fixed value of $\mathrm{Var}(\epsilon)$ as $\mathrm{Var}(X)$ increases the $R^2$ approaches 1.

This extends easily if the slope isn't equal to 1--the important assumption is that $\mathrm{Var}(X)$ and $\mathrm{Var}(\epsilon)$ are uncorrelated.

I find simulation a nice way to understand things too, you can see the effect with the following R code which simulates data for various values of $\mathrm{Var}(X)$ and $\mathrm{Var}(\epsilon)$, fits models, extracts the R squared values, and plots the results in a heatmap.

rsqd <- function(varx = 10, varresid = 3, n = 30, betax = 2) {
    x <- rnorm(n, sd = sqrt(varx))
    y <- betax * x + rnorm(n, sd = sqrt(varresid))
    return(summary(lm(y ~ x))$r.squared)
}

vx <- 1:20
vr <- 1:20

results <- expand.grid(vx = vx, vr = vr)
results$rsq <- numeric(nrow(results))

for (i in 1:nrow(results)) {
    results$rsq[i] <- rsqd(varx = results$vx[i], varresid = results$vr[i])
}

library(ggplot2)
ggplot(results, aes(x = vx, y = vr, fill = rsq)) + geom_tile()

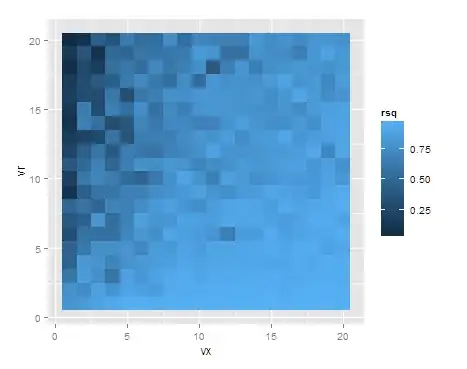
enter image description here

Despite the model always being "right", if the variation in x is small but the residual error is large, the R-squared is quite low (upper left corner). The situation is reversed in the lower right, where the residual error is small compared to the variation of x, and thus compared to the variation explained by x.

Gregor Thomas
  • 1,094
  • 10
  • 21