Is it possible to classify the points inside a square? i.e. if $a \le x \le b$ and $c \le y \le d$ then label is $+1$ otherwise $0$.
Is that possible using SVMs for example?
Is it possible to classify the points inside a square? i.e. if $a \le x \le b$ and $c \le y \le d$ then label is $+1$ otherwise $0$.
Is that possible using SVMs for example?
Your specification of the square as having sides parallel to the boundary makes the problem relatively straightforward - as long as you don't require it to be written as a single SVM, but can settle for something like it.
One very simple estimate of the boundary of the square is for those points which have $+1$ labels to simply take the min and max of $x$ and the min and max of $y$. (It will be too small, of course, but if there are lots of points, not my much.)
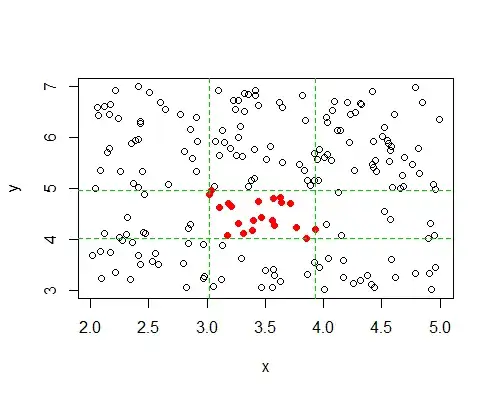
If you then exclude the points with "$0$" labels above the top and below the bottom of that square, you can use SVM or something similar to SVM on the left and the right half of the $x$'s (it's only a 1-D problem for each side! Easy.)
-- so on the right side, for example, you just need the smallest $x$ with a "$0$"-label above the largest "$1$"-label $x$), ...
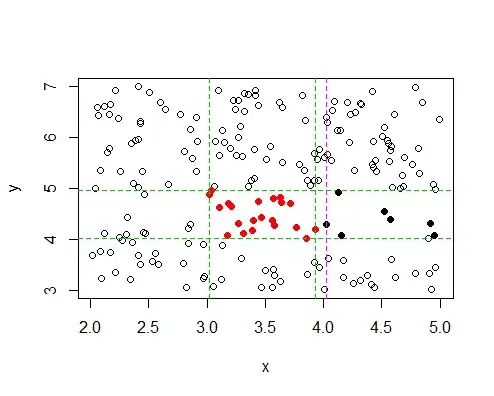
(For your next approximation of the square, you could split the difference between the biggest $1$-x and the next biggest $0$-x:
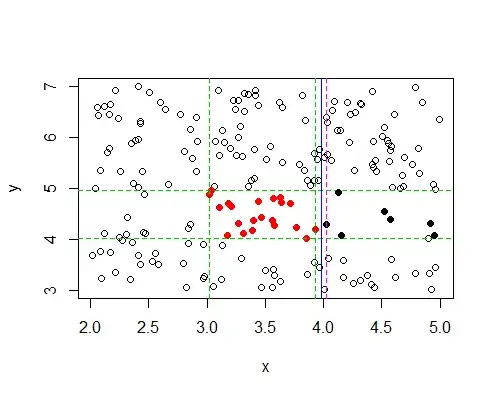
You can then repeat the procedure for the left, top and bottom boundaries. This gives a much better estimate of the boundary than the initial one.)
Of course this won't be exactly square (indeed to this point the algorithm is really for a rectangle with sides parallel to the axes), but the 4 sets of green and pink lines (not all shown) give you boundaries inside which you want to fit the square.
So from there it's a matter of expanding the sides of the blue on the "narrow" direction of the almost-square rectangle and shrinking the "wide" direction, until it's square. Note that you don't shrink/expand the sides evenly; if you want to be SVM-ish, you'd do it so as to even up the amount of remaining "wiggle room" (distance between blue and green or pink, whichever is closer) they have (that is, you'd move the side with the biggest gap between green and pink first, until you reach the size of the next-smallest gap between blue and either green or pink, then change both of those simultaneously until you hit the next smallest gap, and so on).
(With a bit of thinking most of this step can be done very simply.)
So this does some initial processing ($\cal{O}(n)$) to find the inner and outer boxes and the blue rectangle - essentially four trivial "SVM"s, followed by a simple set of expansion/shrinkage calculations to find an actual square.
If there really is a square that perfectly separates the "$1$" and "$0$" cases, that should work quite well and give a nicely SVM-like solution. (If there's not perfect separation, you may need to actually adapt this further in order to minimize misclassification.)
SVM is a linear classifier which means that it can only learn to decide which side of a straight line the points should go. To make a square you obviously need four straight lines. So the short answer is no a linear SVM can not learn a square.
However, you can apply a kernel function to your data to map it into a higher dimension. If you choose the right kernel, there could be a high dimensional line that corresponds roughly to a square in the lower dimensional space.
Think of it like this. Your points lie on a piece of paper and the SVM is a pair of scissors that gets to make one straight cut. You want to capture just the points in the square with that one cut. If the page is flat you can't do it. If you pinch the paper in the middle of the square so that part is raised. you could cut below the pinch and with a single cut select those points.