0

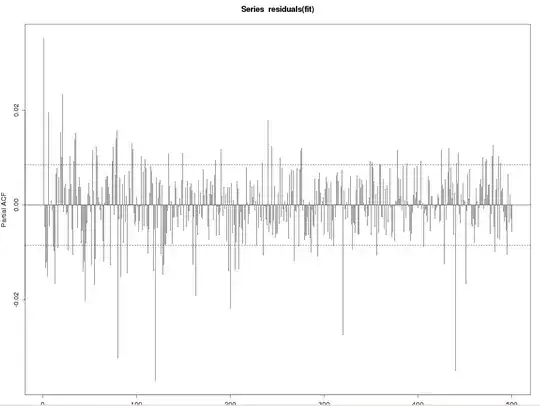
I was using this online calculator to work out McNemar's Test on this data set:

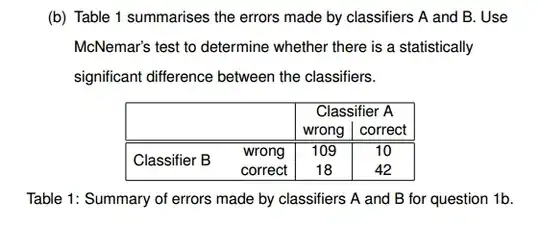
enter image description here

I get the results:

The two-tailed P value equals 0.1859

Chi squared equals 1.750 with 1 degrees of freedom.

Now I understand how to calculate the Chi squared but I have no idea where this P value comes from.

Also how does the P value relate to whether there is a significant difference between classifiers?

If someone could explain this like a program in JavaScript or something it would be so much clearer. Every explanation I see throws jargon all over the place.

Community
  • 1
Joshua Barnett
  • 133
  • 2
  • 6
  • Did you read the [Wikipedia article](http://en.wikipedia.org/wiki/McNemar%27s_test) on McNemar's test? – Scortchi - Reinstate Monica May 17 '14 at 17:17
  • And do you know what p-values are in general - if not see [here](http://stats.stackexchange.com/questions/31) or [here](http://en.wikipedia.org/wiki/P-value). – Scortchi - Reinstate Monica May 17 '14 at 17:23
  • It isn't clear what you need exactly. Benjamin's answer is good (+1), & you may want to read @Scortchi's links to help you understand what a p-value is in general. It may also help you to get a general overview of McNemar's test, I have a fairly comprehensive one here: [What is the difference between McNemar's test & the chi-squared test, & how do you know when to use each?](http://stats.stackexchange.com/a/89415/7290) – gung - Reinstate Monica May 17 '14 at 21:21

1 Answers1

6

Asymptotically the McNemar test statistic follows a chi-squared distribution with 1 degree of freedom. So, if $x_{obs}$ is your observed McNemar test statistic, the $p$ value is

$p = \text{Pr}\left\{ \chi^2_1 > x_{obs}\right\}$

but perhaps this is all the jargon and what not that you were saying you were confused about. What the statement above is saying is that the $p$ value is a probability calcuated under the chi-squared $(\chi^2_1)$ distribution. You can think of a probability as being an area under a particular curve (think back to integrals in calculus).

The curve in question here is the chi-squared density enter image description here

The $p$ value is the blue shaded area under the curve I have plotted.

The curve is defined by: $f(x)=\dfrac{e^{-x/2}}{\sqrt{2x}\Gamma(1/2)}$

Now sure you can try to calculate this by hand to get p-value but most programming languages have built in functions to calculate are under density curves. In R you can do this:

> pchisq(1.75, df=1,lower.tail=FALSE)
[1] 0.1858767
bdeonovic
  • 8,507
  • 1
  • 24
  • 49
  • 1
    Sorry, are you sure that it is a _two-sided_ p-value? – Sergio May 17 '14 at 21:13
  • The p value noted in OP's question looks like one-sided because it matches the one-sided calculation i did in R. – bdeonovic May 17 '14 at 21:24
  • I'd say that it _is_ one-sided, because the chi-squared support is $[0,+\infty]$, so `pchisq(-1.75,1)=0`. Am I wrong? – Sergio May 17 '14 at 21:29
  • who said anything about -1.75? – bdeonovic May 17 '14 at 21:36
  • I mean: where is the _other_ side? – Sergio May 17 '14 at 21:45
  • [This section](http://en.wikipedia.org/wiki/One-_and_two-tailed_tests#History) of the Wikipedia article about one- and two-sided tests expounds my doubt. – Sergio May 17 '14 at 21:57
  • I guess you can consider it a one-sided p value then if that makes you feel better. – bdeonovic May 17 '14 at 22:31
  • 2
    I'd fell better if $p=2\text{Pr}(\chi_1^2>1.75)=0.1859$ ;-) – Sergio May 17 '14 at 22:37
  • 1
    Regardless of semantics (is the test two-sided because it has power against departures from the null hypothesis in either of two directions, or one-sided because one tail area of the test statistic's density gives its size?) the expression $p = 2\text{Pr}\left\{ \chi^2_1 > x_{obs}\right\}$ is simply wrong - out by a factor of 2 as @Sergio says. – Scortchi - Reinstate Monica May 18 '14 at 00:29
  • I'm confused so am I not supposed to work out P? I'll post the full question. Is there no concrete formula for working out P in an exam? – Joshua Barnett May 18 '14 at 11:24
  • yeah you most likely won't be able to compute the p-value by hand. It requires doing quite a complex integral in most situations – bdeonovic May 18 '14 at 12:45