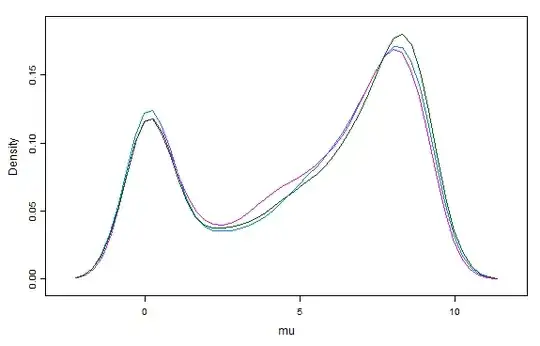
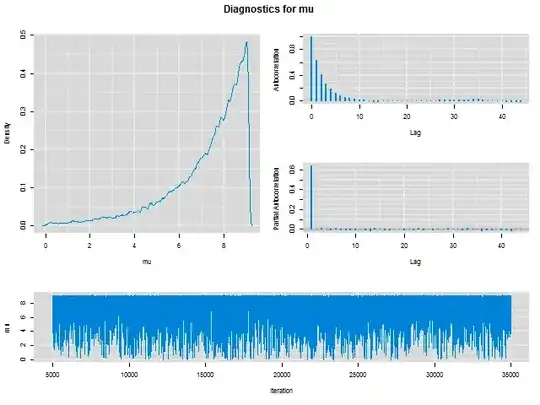
I'm trying to fit a generalised pareto distribution to a simulated dataset using JAGS and runjags. When doing so, I get very strange density and mixing plots for the mu parameter. The sigma and xi parameters are estimated as expected.
How should I interpret these plots, and proceed to fix my model? The plot and a reproducible model are below.
# Simulate gpd
require(evir)
N <- 1000
set.seed(1984)
x <- rgpd(N, xi = 0.5, mu = 5, beta = 2000)
# fit distribution using JAGS
require(runjags)
require(rjags)
library(mcmcplots)
model <- "model {
for (i in 1:N) { #data# N
x[i] ~ dgenpar(sigma, mu, xi) #data# x
}
mu ~ dunif(0.0001, 1e6)
xi ~ dgamma(0.001, 0.00001)
sigma ~ dunif(0.000001, 10000)
#monitor# sigma, mu, xi
}"
results <- run.jags(model, method="rjags", n.chains = 3, modules="runjags", inits = list(list(sigma=1, mu=5, xi=1),
list(sigma=5, mu=1, xi=10),
list(sigma=100, mu=0.1, xi=50)))
load.runjagsmodule()
mcmcplot(results, dir=getwd())
Note that increasing the chain length doesn't solve the problem. After increasing the sample from 4,000 to 400,000, the density for mu isn't anything like a unimodal distribution centred around 5: