MLE of the location parameter in a Cauchy distribution

Question

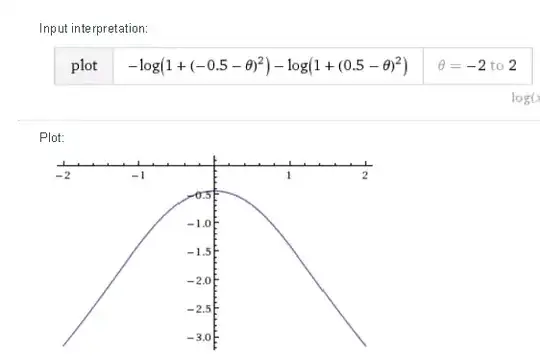
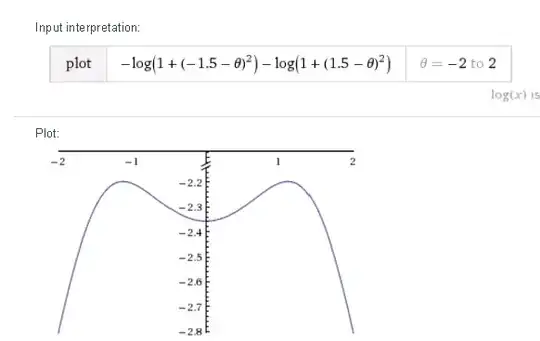
After centering, the two measurements x and −x can be assumed to be independent observations from a Cauchy distribution with probability density function:

$f(x :\theta) = $ $1\over\pi (1+(x-\theta)^2) $ $, -∞ < x < ∞$

Show that if $x^2≤ 1$ the MLE of $\theta$ is 0, but if $x^2>1$ there are two MLE's of $\theta$, equal to ±$\sqrt {x^2-1}$

I think to find the MLE I have to differentiate the log likelihood:

$dl\over d\theta$ $=\sum $$2(x_i-\theta)\over 1+(x_i-\theta)^2 $ $=$ $2(-x-\theta)\over 1+(-x-\theta)^2 $ + $2(x-\theta)\over 1+(x-\theta)^2 $ $=0$

So,

$2(x-\theta)\over 1+(x-\theta)^2 $ $=$ $2(x+\theta)\over 1+(x-\theta)^2 $

which I then simplified down to

$5x^2 = 3\theta^2+2\theta x+3$

Now I've hit a wall. I've probably gone wrong at some point, but either way I'm not sure how to answer the question. Can anyone help?

Answer 1

There is a math typo in your calculations. The first order condition for a maximum is:
\begin{align} \frac {\partial L}{\partial \theta}= 0 &\Rightarrow \frac {2(x+\theta)}{ 1+(x+\theta)^2} - \frac{2(x-\theta)}{ 1+(x-\theta)^2}&=0 \\[5pt] &\Rightarrow (x+\theta)+(x+\theta)(x-\theta)^2 - (x-\theta)-(x-\theta)(x+\theta)^2&=0 \\[3pt] &\Rightarrow 2\theta +(x+\theta)(x-\theta)\left[x-\theta-(x+\theta\right]&=0 \\[3pt] &\Rightarrow2\theta -2\theta(x+\theta)(x-\theta) =0\Rightarrow 2\theta -2\theta(x^2-\theta^2)&=0 \\[3pt] &\Rightarrow2\theta(1-x^2+\theta^2)=0 \Rightarrow 2\theta\big(\theta^2+(1-x^2)\big)&=0 \end{align}

If $x^2\leq 1$ then the term in the parenthesis cannot be zero (for real solutions of course), so you are left only with the solution $\hat \theta =0$.

If $x^2 >1$ you have $2\theta\big[\theta^2-(x^2-1)\big]=0$ so, apart from the candidate point $\theta =0$ you also get

$$\frac {\partial L}{\partial \theta}= 0,\;\; \text{for}\;\;\hat \theta = \pm\sqrt {x^2-1}$$

You also have to justify why in this case $\hat \theta =0$ is no longer an MLE.

ADDENDUM

For $x =\pm 0.5$ the graph of the log-likelihood is

while for $x =\pm 1.5$ the graph of the log-likelihood is,

Now all you have to do is to prove it algebraically and then wonder "fine -now which of the two should I choose?"

Answer 2

Just to record a variant on the above calculation with a couple of shortcuts:

From $\frac{x-\theta}{1+(x-\theta)^2}=\frac{x+\theta}{1+(x+\theta)^2}$ we see that the function $g(y)=\frac{y}{1+y^2}$ takes the same value at $y_1=x-\theta$ and $y_2=x+\theta$, hence so does $\frac{1}{g(y)}=y+\frac{1}{y}$. This function is 2 to 1 (except at $y=\pm 1$) so either $y_1=y_2$ and $\theta=0$ or $y_1=\frac{1}{y_2}$ so $y_1y_2=1$ i.e. $x^2-\theta^2=1$, i.e. $\theta=\pm \sqrt{x^2-1}$ (of course this can happen only if $|x|\geq 1$; if $|x|=1$ the two cases collapse to one and the 3 solutions coincide).

Now, the inverse of likelihood is a degree 4 polynomial in $\theta$, and always positive. So if it has a single extremum (as it does in $x\leq 1$ case) that is a minimum -- i.e. the likelihood has a maximum (at $\theta=0$). If (as in $x>1$ case) it has 3 distinct extrema they must be local min, local max, and local min. So the likelihood has local max, local min, and local max. By symmetry, the values at the two local maxima $\theta=\pm \sqrt{x^2-1}$ are the same, so they are both global maxima.