I have some analysis that compares relative velocity shifts between regions. I have a representative sample below (in reality there are more regions -- this is for clarity).
Assume that I have a dataset with 4 regions -- and the possibility of a relative velocity shift between all four. The only method that I have for determining this relative shift involves a process that forces one of the regions to have a shift of "zero" -- and the other values to shift relative to that.
This means that the y-intercept is arbitrary, but the relative y-values between data points is still important. The plot below shows an example of what I'm doing:
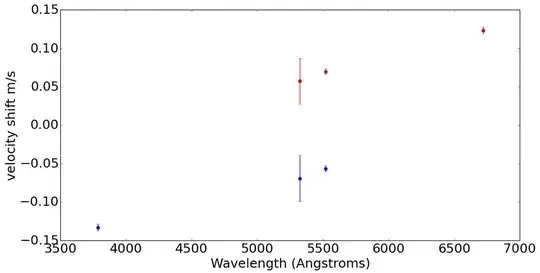
This plot shows the result of finding the relative shifts by alternately setting the first region to zero (red); and the last region to zero (blue). As you can tell, the slope is the same between the two measurements. I also have an error estimate for each point not set to be zero.
I want to fit for the slope across all of the regions.
My question is: is there a statistically robust way to combine this into one fit? Or to fit two linear regressions with independent y-intercepts but tied slopes? Is there another way to think about this entirely?