2

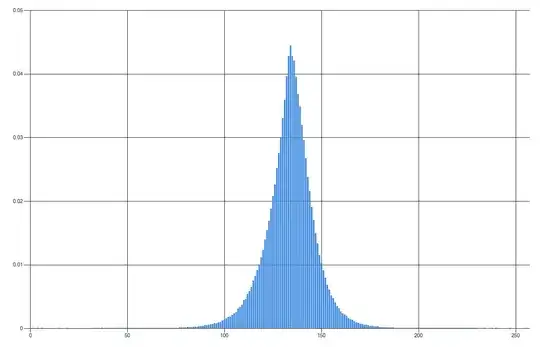
I am doing some signal processing and I have a histogram which has a bell shape when there is only noise in the signal. (I have been advised that this is to be expected due to the central limit theorem)

Histogram

However when the signal that I am looking for is present

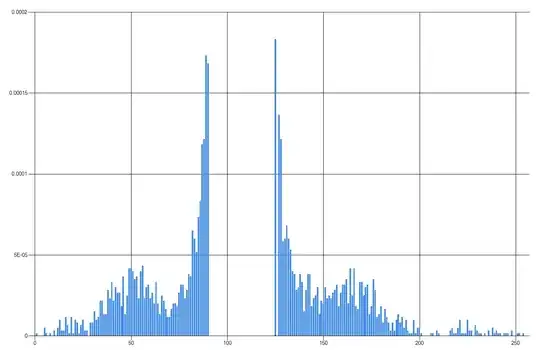
The shape of the histogram changes to With Signal

Note that I have removed the bars in the middle because they are so high it makes it hard to see the detail at the base of the curve.

I would like a test to discriminate between these two cases.

I am aware that there are some tests for normality however I am unsure of how appropriate they are in this case as explained here.

One approach that I have considered is testing the smoothness

$\int_{-\infty}^{\infty}{[f''(x)]^2 dx}$

where f is the normal distribution

EDIT

As Glen_b sugested, I tried the Anderson Darling Test

float[] sortedYs;
sortedYs = Hist.OrderBy(a => a).ToArray<float>();
float[] cdf = new float[sortedYs.Length];

MathNet.Numerics.Distributions.LaplaceDistribution ld = new MathNet.Numerics.Distributions.LaplaceDistribution(U, (b));
for (int i = 0; i < sortedYs.Length; i++)
{
    cdf[i] = (float) ld.CumulativeDistribution(sortedYs[i]);
}

float AD = 0;
for (int i = 0; i < cdf.Length; i++)
{
    AD -= (float)((2 * (i + 1) - 1) * (Math.Log(cdf[i]) + Math.Log(1 - cdf[cdf.Length - 1 - i])));
}
AD /= cdf.Length;
AD -= cdf.Length;
AD *= (float)(1 + (0.75 + 2.25 / cdf.Length) / cdf.Length);

(I'm using C# and Math.Net) I'm still not quite sure if this is how anderson darling works. (about 8000 - 14000 for bubbly, about 4000- 12000 for non bubbly). Its also probably worth noting that I have quite a large data set, since my images have 1920*1080 pixels.

The AD value calculated is much higher for moving video frames.

The smoothnes calculation is done by estimating $\int_{-\infty}^{\infty}{[f''(x)]^2 dx}$

using the raw data for f and then by doing the same estimate but using a laplace distribution (using sample mean and b) for f

I find the difference of these two estimates.

I am getting about 0.01 and less for no motion, and higher for moving images. However there is overlap in these categories as well so its not as reliable as I would like yet.

EDIT

I'm going to post some more histograms

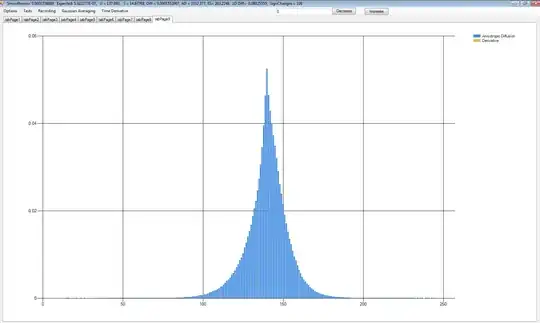
No Motion no motion

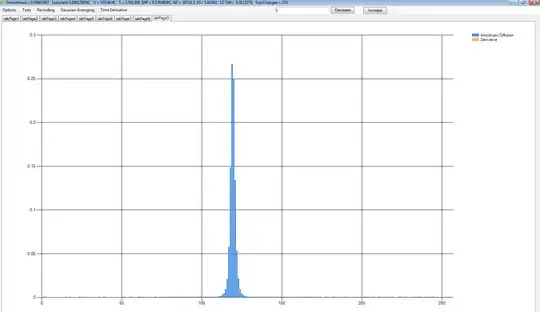
Motion Present motion

I was looking at the noise in the tails all this time, but if I step back and look at the whole histogram, it can be seen that images with motion have a conspicuously lower variance in their histogram than images without motion.

I think this might be partially due to the way pixels are categorised into bins in a histogram. (I'm using opencv and emgu so I will have to look at the source code for more clues here). Images with motion actually have a wider spread of gray scale values than images with no motion. However when calculating the histogram, the pixels have to be placed in bins from 0 to 255. So an image with widely varying grayscale values has lower resolution bins. And so, more pixels get placed in the same bin, even if they a bit different. This does kind of ruin my data, but at the same time, its an effect that I can take advantage of too.

Community
  • 1
sav
  • 187
  • 1
  • 1
  • 10
  • 1
    That first diagram plainly isn't showing something normally distributed. It looks more like it's approximately Laplace (double exponential). At a reasonable sample size any decent test for normality would reject your base case. – Glen_b May 15 '14 at 04:25
  • Thats very interesting. The graph is actually the frequency histogram of an image, I have performed some background subtraction so that when something in the video moves I get the second histogram. When there is no movement, I get a more or less blank image with some noise which results in the fist histogram. – sav May 15 '14 at 04:41
  • 1
    Might you consider a two-sample Anderson-Darling like statistic (rather than Kolmogorov-Smirnov, because it puts more emphasis on the tail, where your interest seems to lie) -- that is, to look at the difference in distribution between a blank image and the other image without specifying the distribution of either? – Glen_b May 15 '14 at 04:49
  • I should probably also mention that as the video plays, the mean and variance of the histogram seems to vary. – sav May 15 '14 at 05:14
  • 1
    You appear to have carried out two one-sample A-D tests. If that's what you did, that wasn't my suggestion. – Glen_b May 18 '14 at 23:31
  • If you have a distribution that changes over time, you have take account of that if you want to use data across different times. – Glen_b May 18 '14 at 23:33
  • I hope this is the correct paper to be looking at http://www.cithep.caltech.edu/~fcp/statistics/hypothesisTest/PoissonConsistency/ScholzStephens1987.pdf – sav May 22 '14 at 05:59
  • I should also add that part of the process of creating the histogram involves converting an image of double to an image of byte. – sav May 22 '14 at 07:42
  • I've described the binning aspect of the problem here http://stats.stackexchange.com/questions/99777/calculating-the-variance-of-the-histogram-of-a-grayscale-image – sav May 23 '14 at 04:19

2 Answers2

1

The main problem I had to solve here was choosing the appropriate bin size.

I found this paper by David Scott which gave me a useful formula.

$h = 3.49 s n^{-1/3}$

where s is standard deviation and n is the number of samples.

This one worked quite well for me and was derived assuming normally distributed data. I also tried deriving an equation based on a Laplace distribution but the results were not as good in my case.

sav
  • 187
  • 1
  • 1
  • 10
0

Use the spectrum.test function in the ts.extend package

Your question does not specify how you got this transformation of your signal, and I have little to say about it in the absence of further information. In any case, it is possible to test for a signal in noise (without assuming that the noise is normally distributed) using a "permutation-spectrum test". This is an extension of Fisher's test for detecting a signal in white noise. The test operates on the time-series rather than the transformation you have given, and it is quite simple to implement.

The test is implemented in the spectrum.test function in the ts.extend package in R. Here is an example where we generate data with a periodic signal and then test for the presence of the signal. The test output and resulting plot easily detects the signal.

#Load the package
library(ts.extend)

#Generate mock data
set.seed(1)
m      <- 100
SIGNAL <- 0.8*sin(0.3*(1:m))
NOISE  <- rnorm(m)
SERIES <- SIGNAL + NOISE

#Conduct permutation-spectrum test
TEST <- spectrum.test(SERIES)
TEST
        Permutation-Spectrum Test

data:  real time-series vector SERIES with 100 values
maximum scaled intensity = 3.6428, p-value = 0.000208
alternative hypothesis: distribution of time-series vector is not exchangeable 
(at least one periodic signal is present)

#Plot the test results
plot(TEST)

enter image description here

Ben
  • 91,027
  • 3
  • 150
  • 376