1

Most of you will have been entertained by the recent blog post showing how random things in the world correlate without, of course, necessarily being causally related.

Looking at those graphs, I was wondering in my mind whether, for two vectors X and Y to be correlated, it is the difference or the ratio between their respective elements that needs to be relatively constant between elements. In the graphs, the two variables are always on very different scales, and so it is the difference that is constant rather than the ration.

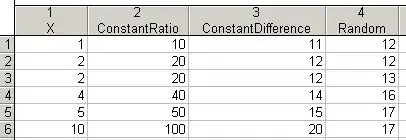
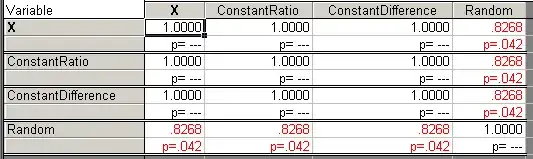
Did a quick check in Statistica and turns out that either is sufficient: enter image description here enter image description here

Or am I making a mistake here?

Looked at the definition of Cov(X,Y) but didn't help me understand better.

Community
  • 1
z8080
  • 1,598
  • 1
  • 19
  • 38
  • 2
    When X and Y are both centered variables, $r$ is [exactly related](http://stats.stackexchange.com/a/36158/3277) to the summed squared difference (i.e. squared euclidean distance). Also, since $r$=1 if X=k*Y+c, if you z-standardize both variables then it appeares that $r$=1 if X-Y = constant 0. – ttnphns May 15 '14 at 07:01
  • I didn't realise that if X and Y are linearly dependent, then r=1! This explains why having a constant difference (c, while k=1) OR a constant ratio (k) makes r=1. Thanks!! – z8080 May 15 '14 at 14:34

1 Answers1

1

Neither a constant difference nor a constant ratio are needed. Consider $X=(1,2,3,\dots,10)$ and $Y=X^2$. Their differences are $0,2,6,\dots,90$, their ratios are $1,2,3,\dots,10$, but their correlation is $0.97$.

Sergio
  • 5,628
  • 2
  • 11
  • 27