11

Say I have a large sample of values in $[0,1]$. I would like to estimate the underlying $\text{Beta}(\alpha, \beta)$ distribution. The majority of the samples come from this assumed $\text{Beta}(\alpha, \beta)$ distribution, while the rest are outliers that I would like to ignore in the estimation of $\alpha$ and $\beta$.

What is a good way to proceed about this?

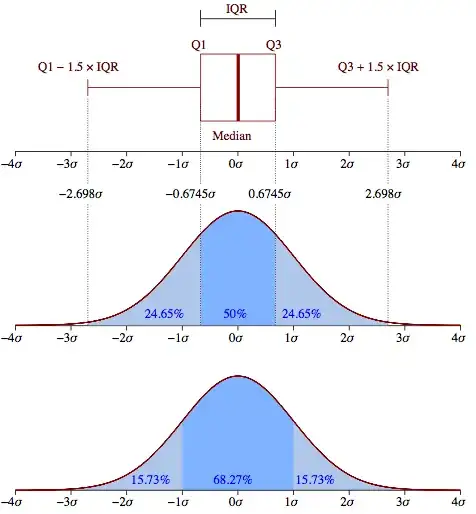
Would the standard: $\text{Inliers} = \left\{x \in [Q1 - 1.5\, \text{IQR}, Q3 + 1.5 \,\text{IQR}] \right\}$ formula used in boxplots be a bad approximation?

What would a more principled way of solving this? Are there any particular priors on $\alpha$ and $\beta$ that would work well in this type of problem?

                    enter image description here

Amelio Vazquez-Reina
  • 17,546
  • 26
  • 74
  • 110
  • consider the answer posted [here](http://stats.stackexchange.com/questions/13086/is-there-a-boxplot-variant-for-poisson-distributed-data/13429#13429). Once the outliers have been flagged, remove them, and use MLE distribution fitting on the remaining observations. It will be more precise for the reasons explained at the link. – user603 May 14 '14 at 17:55

1 Answers1

3

A more systematic way to deal with this problem would be to use an explicit mixture model, with a specification of the distribution of the 'outliers'. A simple form would be to use a mixture of a beta distribution (for the points you're interested in) and a uniform distribution (for the 'outliers'). By modelling the data as a mixture distribution you could get estimates of $\alpha$ and $\beta$ that automatically take into account the fact that some of the points may be outliers.

To solve this problem using a mixture model, let $\phi$ be the probability of an 'outlier' and assume you have IID values $X_1, ..., X_n \sim \phi \cdot \text{U}(0, 1) + (1- \phi) \cdot \text{Beta}(\alpha, \beta)$. The likelihood function for the observed data is:

$$L_\boldsymbol{x}(\alpha, \beta, \phi) = \prod_{i=1}^n \left( \phi + (1 - \phi) \frac{\Gamma (\alpha + \beta)}{\Gamma(\alpha) \Gamma(\beta)} x_i^{\alpha - 1} (1-x_i)^{\beta - 1} \right).$$

You could proceed from here using either classical MLE or Bayesian estimation. Either will require numerical techniques. Having estimated the three parameters in the model, you would then have an estimate of $\alpha$ and $\beta$ that automatically incorporates the possibility of outliers. You would also have an estimate of the proportion of outliers from the mixture model.

Ben
  • 91,027
  • 3
  • 150
  • 376