ARIMA model selection

Question

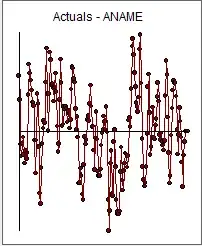
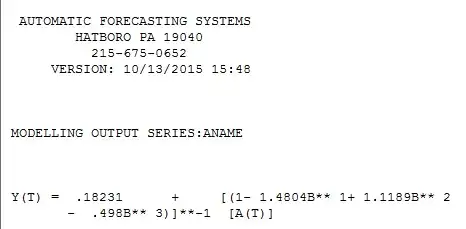
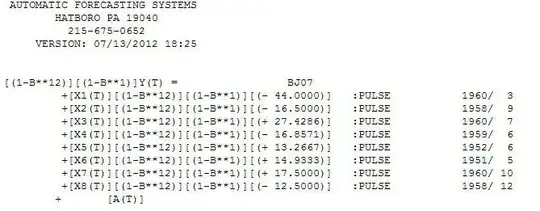
I am trying to find a model for the data below. I cannot decide whether the data is stationary or not. I do not want to take differences unnecessarily . I put results of the models below. I think ARIMA(0,1,3) is best model because AIC is lowest .What do you think?

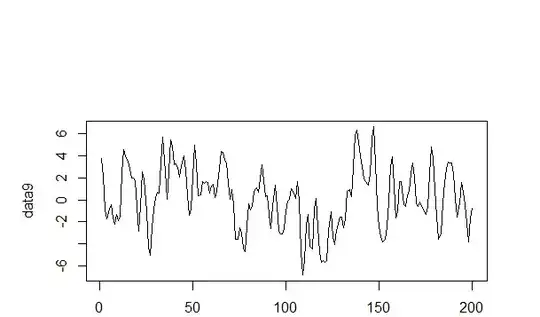
[1]  3.78937537  2.15208174 -0.89160064 -1.73332645 -0.83482963 -0.41333144
  [7] -1.63430676 -2.20777662 -1.35331581 -1.87955944 -1.49146551  2.49103865
 [13]  4.58664031  3.98372753  3.49151073  2.80024199  1.98523634  2.00031840
 [19]  1.74083830 -0.61761601 -2.88803617 -0.61886754  2.57402611  1.89283706
 [25] -1.07544734 -4.26161203 -4.99017725 -2.51596702 -0.86119264  0.18702439
 [31]  0.71532140  0.57777386  3.35966227  5.69130104  2.56164573  0.03846258
 [37]  2.58144870  5.42012156  4.91012242  3.19472611  3.25517135  2.99351748
 [43]  2.04710036  3.00828776  3.97207225  2.69966884  0.34465355 -1.43062776
 [49] -0.86202757  2.17878741  4.93325672  3.31060112  0.35611519  0.46807870
 [55]  1.66712453  1.51650578  1.67546667  1.55933575  0.63240519  1.28472844
 [61]  1.38605161  0.18651983  0.79863043  2.87366933  4.44551597  4.30870925
 [67]  3.60995558  3.35830065  1.53707953  0.08623542  0.97667994 -0.42280994
 [73] -3.58389281 -3.55316081 -2.55628493 -3.04211427 -4.34371036 -4.72314008
 [79] -2.32487771 -0.38168241 -0.89383414 -0.58963196  0.77158269  1.07205599
 [85]  0.72950780  1.88525945  3.16151643  1.72134300  0.31586665  0.34106233
 [91] -1.31065867 -2.64398487 -0.47188919  1.33507435 -0.55269545 -2.74748555
 [97] -3.06504226 -3.07342362 -2.60963150 -0.96491699 -0.11554423  0.07801436
[103]  1.03953592  0.63529388  0.10310775  1.67245060 -0.08355651 -4.69707317
[109] -6.83755810 -5.48216561 -2.18589446 -1.34859551 -4.25464826 -4.44676908
[115] -0.72380753  0.10925230 -2.45630323 -4.70575810 -5.66265488 -5.50397286
[121] -5.64958955 -5.48545360 -2.79058869 -1.10528812 -3.35615732 -4.07432989
[127] -2.73350349 -2.21617434 -1.52494934 -1.58548803 -2.49378602 -1.69527130
[133]  0.74873392  0.90627894  0.30555834  2.92103049  5.83058432  6.36187212
[139]  5.22905256  4.00941490  3.03523663  1.93713509  1.67471721  1.32443755
[145]  2.32354111  5.63314456  6.62253314  3.30169519 -0.53170457 -2.45563036
[151] -3.33244848 -3.77673941 -3.54203732 -2.45898416 -0.16490056  3.04228090
[157]  3.92168880  1.24849940 -1.63284318 -1.07538492  1.65080853  1.66193852
[163] -0.42635583 -0.55887445  0.41598367  0.86267051  2.37980973  3.33955626
[169]  2.06034558 -0.23641280 -0.58777692 -0.15430770 -0.71699361 -0.97577373
[175] -1.32154837 -0.63551008  2.42331965  4.81896345  3.87979306  0.95525157
[181] -1.50232828 -3.57249760 -3.03952767 -0.28938790  1.58862094  2.81297712
[187]  3.46355587  3.35284181  3.33816359  2.39696945  0.09838492 -1.57887066
[193] -0.24116984  1.61287955  0.67580375 -0.41342769 -2.12526810 -3.82541756
[199] -1.64497472 -0.73523703

Model fitting

Call:
arima(x = data9, order = c(0, 1, 3))

Coefficients:
         ma1      ma2      ma3
      1.0905  -0.4871  -0.6763
s.e.  0.0750   0.1390   0.0760

sigma^2 estimated as 0.8477:  log likelihood = -268.35,  aic = 542.7

Call:
arima(x = data9, order = c(1, 0, 1))

Coefficients:
         ar1     ma1  intercept
      0.7070  1.0000     0.2048
s.e.  0.0497  0.0213     0.4983

sigma^2 estimated as 1.097:  log likelihood = -296.55,  aic = 599.11

Answer 1

You could try R forecast package function auto.arima, which selects ARIMA models automatically, in this instance it chose ARMA(2,0,2) with the lowest possible AIC.

With regards to differencing, what you may be observing is a local time trend, which can be corrected using an appropriate outlier handling method based on Tsay's work. There is a specialist in this website @Irishstat who can provide much better insight than me on why you dont need differencing on this data. To my knowledge only SAS/SPSS/Autobox have the ability to detect these type of outliers.

auto.arima(mydata)
Series: mydata 
ARIMA(2,0,2) with zero mean     

Coefficients:
         ar1     ar2     ma1     ma2
      0.2562  0.1132  1.8443  0.8939
s.e.  0.0949  0.0933  0.0467  0.0436

sigma^2 estimated as 1.028:  log likelihood=-289.96
AIC=589.91   AICc=590.22   BIC=606.41

Answer 2

Thanks @forecaster for the nice words about me and AUTOBOX ( a piece of software that I have helped to develop ). The data ; the final model is a (3,0,0) with statistics here . A plot of the residuals is here with Actual/Fit Forecast here . The fact that there were no pulses or level shifts or local time trends suggests that the data might have been created via a simulation for teaching purposes.

Answer 3

Just by looking at the data it is hard to say that it is nonstationary. However, if you run the command [h,p]=adftest(data,'lags',[0:20],'model','TS') in MATLAB, the results are mixed:

h =

Columns 1 through 13

 1     1     1     1     1     1     0     1     0     1     0     1     1

Columns 14 through 21

 0     0     0     0     0     0     0     0

For lags higher than 6 it doesn't reject the unit root in Augmented Dickey-Fuller test with trend-stationary model. This means that the series may have the time trend.

Also, you wrote you don't want to do differencing unnecessarily, but ARIMA(0,1,3), the best fit according to you, does the first order differencing. So, this might be another indication that there is indeed nonstationarity. However, I don't think that based solely on these 200 points nonstationarity can be reliably established. You need to know more about the data, the context, the background, which will provide you with information exogenous to 200 numbers.