5

I am trying again to explain my problem, and I have more concrete results. I have tried every potentially relevant test I can find, and none seem to work quite right.

The question is illustrated here:

enter image description here

The actual data are protein sequences. I have two categories of specimens, shown by the black and grey circles, and many positions of genes, shown by the colored squares. I want to find which of the gene positions correlate with the specimen categories. For example in row 1, there is perfect correspondence. Nearly all metrics pick up this signal. In row 5, the genes are exactly evenly distributed between the traits, and again most metrics get this. However, in case 4, there is zero predictive power for that trait, (every position has to have one or the other value, so expected value should be 1), but most tests report a high value.

I have a script which calculates metrics for test cases and actual data, and some of these results are illustrated below. The data set has been rotated so the rows are now columns, and the two categories are indicated by the colors of the letters, with two black rows and 4 grey rows.

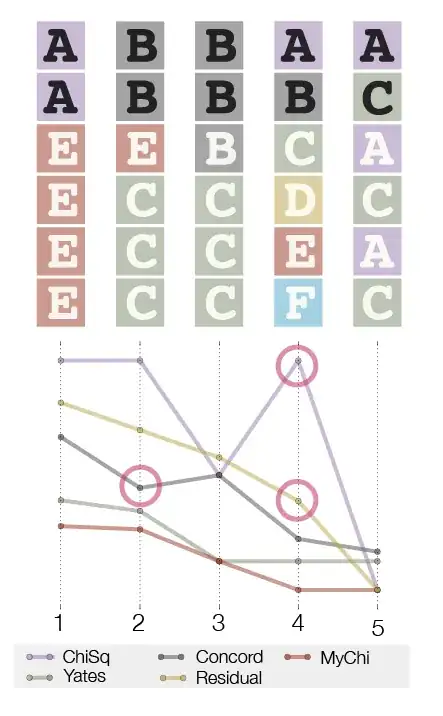
enter image description here

Yates-corrected Chi-square, Mutual Information, Fisher's exact test, Concordance (with some assumptions), etc, all fail on case 4, and some of them give case 2 an equal value to case 1, or score case 3 higher than case 2.

I came up with a metric (MyChi, the rust-colored line above) which is an attempt at a one-tailed Chi-square (only adds values higher than expected, and not lower), normalized by the number of traits present, and not counting the singleton traits. It works pretty well (the columns in the second figure are ordered by how well they "should" score), but I am leery of just making up a test.

The actual data also have a limitation that there will always be lots of zeroes and ones in a contingency table, so many of the standard tests are not recommended. Although there are many rows per sample (and I would like to figure out a way to sum the scores from all rows into one metric), there might only be 20 values for each row.

Does anyone have a recommendation for a test to address this analysis?

Community
  • 1
beroe
  • 133
  • 7
  • 1
    I'm confused, and took a look at your earlier question, which helped somewhat, but didn't answer all my questions. Then I reread and have a better idea of what's going on. In the future I suggest making it very clear which parts of your figures are the data and which parts are the analysis (in this case, your analysis of the different metrics). – Hao Ye May 09 '14 at 23:21
  • "However, in case 4, there is zero predictive power for that trait, (every position has to have one or the other value, so expected value should be 1), but most tests report a high value." I'm not sure what you want the result to be in this case -- knowing what kind of specimen you have (black or grey) is very informative about the gene position (if black, then A or B, if grey, then C, D, E, or F). – Hao Ye May 09 '14 at 23:28
  • Thanks @HaoYe. Your second question exactly captures my problem with the standard tests. I don't need to know if the kind is related to a specific trait, but whether the traits are clustered with the kind. In case 4, it doesn't matter if black = C,F or A,B. I am looking for cases where the state (A-F) is *grouped* according to state (black-grey). This is what I am having a hard time explaining. One approach I considered was to find the number of identical states for each category *which were different from the other category* and compare those values. – beroe May 09 '14 at 23:42
  • Ok, in that case, would it be safe to say that you would like the metric to give equivalent results for cases 4 and 5, because there is no 1:1 from specimen_type to gene position. Also, is the kind of specimen always a binary variable (black or grey)? – Hao Ye May 09 '14 at 23:56
  • There could be conceivably 3 or more kinds of specimen, but I would be more than happy a good solution for the binary case. – beroe May 10 '14 at 21:22

1 Answers1

2

It appears that Case 4 is a case of "perfect separation" - i.e. each gene position is uniquely related to one of the two specimen categories. If this is correct, then this is a known problem with categorical variables. Look up these CV post How to deal with perfect separation in logistic regression? and Seeking a Theoretical Understanding of Firth Logistic Regression

but there are also others.

Also, a search on the web will provide many links and references.

Community
  • 1
Alecos Papadopoulos
  • 52,923
  • 5
  • 131
  • 241
  • Thanks. I ran my test data through `glmnet` and `elasticnet`, but can't make sense of the results to tell if it would work. `enet` with Lasso fit gives decent coefficients, perhaps, but they seem to treat the factors as numerically scaled (factor 5>>1) rather than as categories? – beroe May 10 '14 at 21:30