13

According to The SAGE Encyclopedia of Social Science Research Methods…

[a] ceiling effect occurs when a measure possesses a distinct upper limit for potential responses and a large concentration of participants score at or near this limit. Scale attenuation is a methodological problem that occurs whenever variance is restricted in this manner. … For example, a ceiling effect may occur with a measure of attitudes in which a high score indicates a favorable attitude and the highest response fails to capture the most positive evaluation possible. …The best solution to the problem of ceiling effects is pilot testing, which allows the problem to be identified early. If a ceiling effect is found, [and] the outcome measure is task performance, the task can be made more difficult to increase the range of potential responses.1 [emphasis added]

There seems to be lots of advice and questions (and here) dealing with analysing data which show ceiling effects similar to that described in the quote above.

My question may be simple or naive, but how does one actually detect that a ceiling effect is present in the data? More specifically, say a psychometric test is created and is suspected to lead to a ceiling effect (visual examination only) and then the test is revised to produce a greater range of values. How can it be shown that the revised test has removed the ceiling effect from the data it generates? Is there a test which shows that there is a ceiling effect in data set a but no ceiling effect in data set b?

My naive approach would be to just examine the distribution skew and if it's not skewed, conclude that there is no ceiling effect. Is that overly simplistic?

Edit

To add a more concrete example, say I develop an instrument which measures some latent trait x which increases with age but eventually levels off and starts to decline in old age. I make the first version, which has a range of 1—14, do some piloting, and find that it seems there may be a ceiling effect (a great number of responses at or near 14, the maximum.. I conclude this just by looking at the data. But why? Is there any rigorous method of supporting that claim?

Then I revise the measure to have a range of 1—20 and collect more data. I see that the trend more closely matches my expectations, but how do I know that the range of measurement is large enough. Do I need to revise it again? Visually, it seems to be ok, but is there a way of testing it to confirm my suspicions?

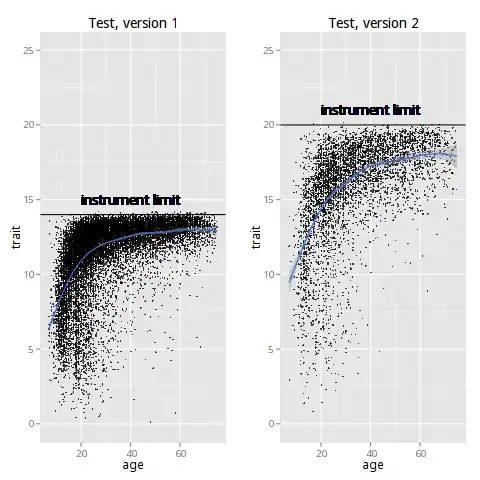
enter image description here

I want to know how I can detect this ceiling effect in in the data rather than just looking at it. The graphs represent actual data, not theoretical. Expanding the range of the instrument created a better data spread, but is it enough? How can I test that?

1 Hessling, R., Traxel, N., & Schmidt, T. (2004). Ceiling Effect. In Michael S. Lewis-Beck, A. Bryman, & Tim Futing Liao (Eds.), The SAGE Encyclopedia of Social Science Research Methods. (p. 107). Thousand Oaks, CA: Sage Publications, Inc. doi: 10.4135/9781412950589.n102

Community
  • 1
ceiling
  • 131
  • 1
  • 6
  • 4
    To make progress, one would have to come up with an operational definition of "ceiling effect." Doing that in general could be problematic: after all, almost any measured quantity cannot realistically exceed some value, such as 100% in a test score or chemical concentration, the upper limit of what an instrument can read, and so on, so arguably almost all data are subject to some inherent upper bound. So, although the intended meaning of "ceiling effect" is intuitively clear from your nice examples, you can help us out by clarifying exactly *what* needs to be "removed" from your data, and why. – whuber May 07 '14 at 14:28
  • 1
    @whuber you are right that the term is used in several different ways, but in this case, I'm talking about making a ruler long enough to exceed all of the things I want to measure. When creating tests, you surely want to include enough items of a range of difficulties so that no one gets 100%, otherwise you won't know whether that person's ability is actually the limit of the test or higher. Nothing needs to be removed from the data, but the instrument needs to be revised until it doesn't yield censored data points. – ceiling May 07 '14 at 14:45
  • Thank you. I'm still not sure what you mean by "ceiling effect," though, because neither of your illustrations shows overt evidence of any kind of censoring--at least not with fixed censoring limits of the kind achieved with a test. In fact, the change from the left to the right panel looks more like a one-to-one nonlinear re-expression of the vertical axis, which would have no effect on any ceiling in the data. This makes me wonder whether you are really concerned about something completely different, such as asymmetry of regression residuals. – whuber May 07 '14 at 14:51
  • @whuber I have added additional information to the question. The data are from two different data sets, but I'm not concerned so much with this specific example, but more in general, how can one use statistics to identify reduced variance near the instrument limits to confirm that a ceiling effect exists or has been eliminated through revision of the instrument. – ceiling May 07 '14 at 15:07
  • Your updated graphics are interesting in that they suggest at least two distinct sources of variation: one is the residual variation in the regression, which is limited by the upper bound of the instrument; but there clearly is another source of error that allows some of the observations actually to *exceed* that instrument upper bound. When an "instrument" is a psychological one--a linear combination of numerically coded survey responses--that second source of variation is usually not present. I wonder what relevance the illustrations really have for the questions. – whuber May 09 '14 at 13:24
  • 1
    @whuber jitter has been added since most of the points overlap. If the graphs don't appear to relate to my question, then obviously I have no idea what I'm talking about. To me, it seems like there is a ceiling effect as described by Hessling, Traxel, & Schmidt, but based on your comments and the complete lack of interest in this question, maybe I'm seeing a problem where there is none. Thanks your your suggestions and insights though. I appreciate it. – ceiling May 09 '14 at 13:43
  • @whuber A bit of thread necromancy here: What about if you could assume the type of distribution for $(trait | age)$ in the example plots? Say that we can assume that the trait is normally distributed and that we have a random sample; If the instrument actually measured values for $(trait | age)$ which are negatively skewed, then there would be some ceiling effect, right? If so, could a normality test be a way to detect ceiling effects? – Johan Falkenjack Jan 18 '17 at 21:03
  • @Johan Ordinarily one doesn't need much of a test: the ceiling effects are usually manifested as a clear, definite upper limit that is either never exceeded or is not exceeded within a margin of error comparable to the instrument's precision. – whuber Jan 18 '17 at 21:20
  • @whuber Sure, but isn't the question rather about whether that limit is high enough? Whether there are more measured points at or near that upper limit than expected with regards to the distribution of the measured trait? This is especially problematic where the measure is discrete, for instance, the number of correct answers on a test. – Johan Falkenjack Jan 18 '17 at 21:37
  • 1
    @Johan I see. In the spirit of your question, it occurs to me that a slight modification of your idea might be a good one. Unless we have reason to suppose the residuals must be normally distributed, we might seek to find a monotone transformation of the response in which the residual distributions are homoscedastic where the response is low and possibly become truncated where the response is high. In other words, perhaps the test ought not to be for *normality* but should look for a *consistent shape and scale* to the response. – whuber Jan 18 '17 at 21:42

3 Answers3

3

First off, I would like to say that both graphs provide clear evidence to me that there is a ceiling effect present. How I would attempt to measure that effect rather than just visually would be to observe that so long as a non-trivial portion of the observations lie near the upper limit of the instrument's range. Typically speaking a ceiling effect will always exist so long as there are a non-trivial portion of test takers who achieve the maximum score on the test.

However, that said, the technology of test analysis has progressed a long way since we needed to directly interpret the scores on a instrument based on the score correct. We can now use Item Response Theory to estimate the item parameters of individual items and use those items to identify subject ability. There of course can be still ceiling effects on a test if we make the test too easy. However, due to the powers of item response theory we should be able to put at least a few items of high enough difficulty in the instrument so as to prevent only but a trivial portion of the population hitting the ceiling.

Thanks for the question. It is very interesting!

Francis Smart
  • 610
  • 3
  • 9
2

I guess a rough and ready way would just be to measure the variance as the scale increases. If this shows a reduction then this is evidence for a ceiling effect and if not there is no ceiling effect. You could make a homogeneity of variance plot. Levene's test could be useful to determine whether variance is sig different at different points on the scale.

user45114
  • 111
  • 6
  • 2
    thanks for the idea. I'll try it, but I expect variance to naturally decrease with age in this case. – ceiling May 08 '14 at 02:50
  • Ceiling, both this answer and your comment appear to confound two distinct concepts. The *scale* variance would reflect the dispersion of repeated independent measurements of a subject; it is supposed not to depend on the subject but possibly to vary with the subject's mean response. The variance to which you and this answer refer is the variance of regression residuals. Although they are related, they are not the same thing. – whuber May 08 '14 at 16:05
  • @whuber thanks for pointing that out. by the way, you still don't see any evidence of a ceiling effect with the update graph and information? I'm quite surprised this question has attracted almost no interest given the multiple questions and answers on analysing data with ceiling effects present. – ceiling May 09 '14 at 05:28
  • Hi. So long as you are plotting variance between subjects as scale increases, rather than within subjects, will this not tell you something about ceiling effects? - can you still use Levene's test to test for significant change in variance as scale increases? or is this only designed to test within subject changes in variance? Should we use a different term to describe the variation of different people's scores as the scale increases other than "scale variance", such as "Variance of residuals"? Can levene's test be used to show that "variance of residuals" is uniform across the scale – user45114 May 11 '14 at 09:52
0

The critical problem in deciding whether a clustering around the highest or lowest point is due to a ceiling/floor effect is whether the values of the cases actually "represent" the value. When ceiling/floor effects do occur, some of the cases, despite assuming the maximum or minimum value, are actually higher/lower than the maximum or minimum value (imagine an adult and a child both finish an extremely simple math test that purported to measure one's math capability, and both scored 100%). Here, the data is censored.

Another scenario is also possible when we use bounded scales such as a Likert-like scale which has inherent upper and lower limits. It is entirely possible that those who scored the highest are indeed worth that score and no differences (such as the math example above) exist among all who scored the highest. In such a case, the data is truncated at the limits, not censored.

Based on the above reasoning, I reckon one should devise a procedure to fit any given dataset with data truncation and data censoring. If the censoring model best fitted the data, I think one may then conclude that a ceiling/floor effect is present.

Candamir
  • 970
  • 8
  • 27
wuy3814
  • 1
  • 1