2

I guess this is similar to this one but not quite the same. Consider I have a distribution that represents a population (e.g., Uniform(0,1)). I separate this interval (0,1) into three equal parts (0-1/3, 1/3-2/3 and 2/3-1). For the population, I will have for each interval 33.333% of data. The graph for the population is presented below.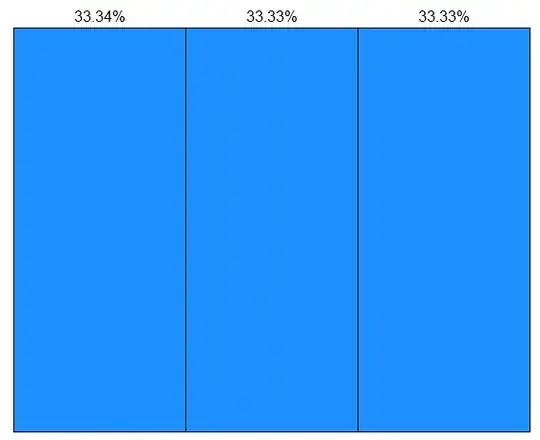Uniform distribution divided into three parts

I need samples that represent the populations "well enough". For example, for Uniform(0,1), I could have a sample with 50,000 elements and a graph as presented below. 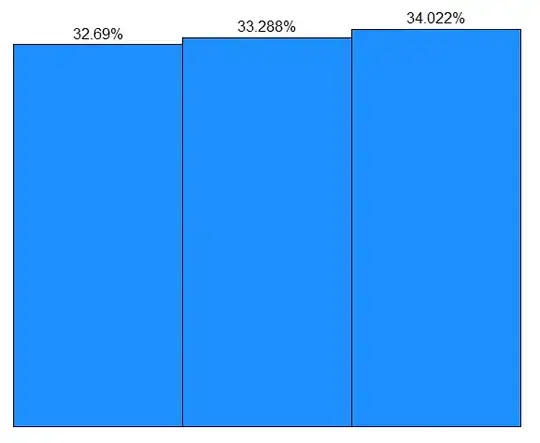Distribution of samples of a Uniform distribution

I could get a huge number of samples (e.g., 100000) if performance was not a significant issue, but it is not the case. I am considering that "well enough" is with 4% margin of error and 95% confidence. So, how to calculate the minimum sample size I need to, with a margin of error of 4% and 95% confidence (for each interval), to represent the population (given that the population size is unknown)?

ps.: with "represent the population" I mean having a graph of samples similar to the graph of the population. In other words, for the example and parameters given, with 95% confidence, none of the bars will be below 31.33% or greater than 35.34%

Community
  • 1
ryouma
  • 21
  • 3
  • 1
    I can't follow your description. What are you going to mix these with? What are you estimating subsequently? What would it mean for whatever estimate you end up w/ afterwards on, say, the 1st third to "represent the population"? Etc. Can you make this more concrete? – gung - Reinstate Monica Apr 29 '14 at 19:19
  • I edited the question. The "mixture" part is not relevant. Let me know if you need more information. Thanks! – ryouma Apr 29 '14 at 21:35
  • This question asks for the sample size needed to assure that the range of a multinomial distribution lies within given bounds with a given confidence. – whuber Apr 29 '14 at 22:21
  • ryouma - can you confirm (or clarify otherwise) if whuber's statement about what you're seeking is correct? – Glen_b Apr 29 '14 at 22:38
  • 1
    @Glen_b, yes. In the example given in the question, I have 3 categories and each category has a fixed success probability of 33.33%. So, it can be considered a multinominal distribution. To generalize the question, it is exactly what you said: calculate the sample size (or number of trials) to assure that the range of a multinomial distribution lies within given bounds with a given confidence. – ryouma Apr 30 '14 at 01:46

0 Answers0