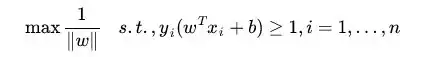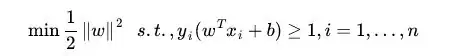Note that $\| w \|$ is nonnegative. Thus $1/\| w \|$ is a monotone decreasing function of $\| w \|$. Minimizing $\| w \|$ is thus equivalent to maximizing $1/\| w \|$. Note here that by "equivalent", I don't mean that the optimal objective value will be the same, but rather that any optimal solution to the first problem will be optimal for the second problem and vice versa.
Since squaring a positive quantity is a monotone increasing transformation, minimizing $\| w \|^{2}$ is equivalent to to minimizing $\| w \|$. Finally, multiplying by $1/2$ has no effect on the set of optimal solutions. Thus
minimizing $(1/2) \| x \|^{2}$ is equivalent to maximizing $1/\| w \|$.
The advantage of minimizing $ (1/2) \| w \|^{2}$ is that it's easy to compute the gradient of this objective function (it's $w$.)