Estimating parameters for a spatial process

Question

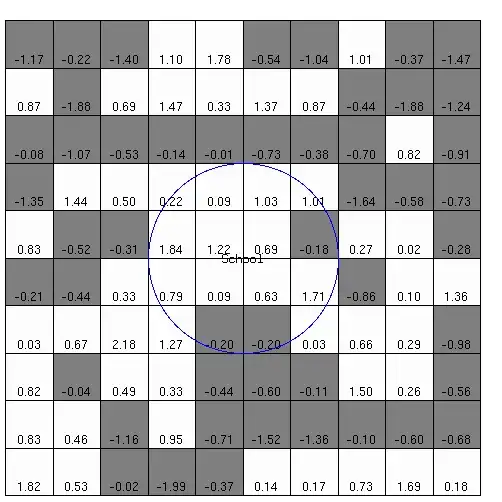
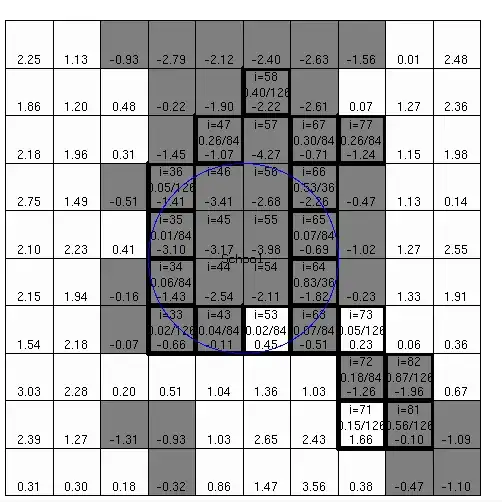
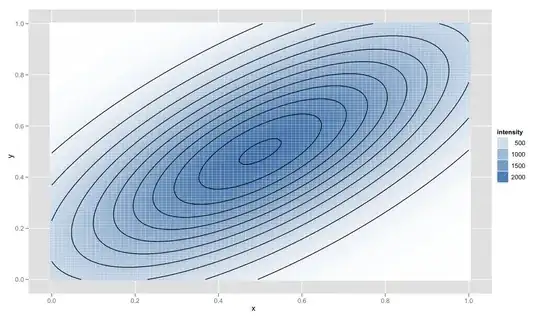
I'm given an $n\times n$ grid of positive integer values. These numbers represent an intensity that should correspond to the strength of belief of a person occupying that grid location (a higher value indicating a higher belief). A person will in general have an influence over multiple grid cells.

I believe that the pattern of intensities should "look Gaussian" in that there will be a central location of high intensity, and then the intensities taper off radially in all directions. Specifically, I'd like to model the values as coming from a "scaled Gaussian" with a parameter for the variance and another for the scale factor.

There are two complicating factors:

• the absence of a person will not correspond to a zero value, because of background noise and other effects, but the values should be smaller. They can be erratic though, and at a first approximation might be difficult to model as simple Gaussian noise.
• The intensity range can vary. For one instance, the values might range between 1 and 10, and in another, between 1 and 100.

I'm looking for an appropriate parameter estimation strategy, or pointers to relevant literature. Pointers to why I'm approaching this problem the wrong way altogether would also be appreciated :). I've been reading about kriging, and Gaussian processes, but that seems like very heavy machinery for my problem.

Answer 1

You can use this module of the pysal python library for the spatial data analysis methods I discuss below.

Your description of how each person's attitude is influenced by the attitudes of the people surrounding her can be represented by a spatial autoregressive model (SAR) (also see my simple SAR explanation from this SE answer 2). The simplest approach is to ignore other factors, and estimate the strength of the influence how surrounding people affect one another's attitudes by using the Moran's I statistic.

If you want to assess the importance of other factors while estimating the strength of the influence of surrounding people, a more complex task, then you can estimate the parameters of a regression: $y = bx + rhoWy + e$. See the docs here.(Methods of estimating this type of regression come from the field of spatial econometrics and can get much more sophisticated than the reference I gave.)

Your challenge will be to build a spatial weights matrix ($W$). I think each element $w_{ij}$ of the matrix should be 1 or 0 based on whether the person $i$ is within some distance you feel that it is required to influence the other person $j$.

To get an intuitive idea of the problem, below I illustrate how a spatial autoregressive data generating process (DGP) will make a pattern of values. For the 2 lattices of simulated values the white blocks represent high values and the dark blocks represent low values.

In the first lattice below the grid values have been generated by a normally distributed random process (or Gaussian), where $rho$ is zero.

In the next lattice below the grid values have been generated by a spatial autoregressive process, where $rho$ has been set to something high, say .8.

Answer 2

Here is a simple idea which might work. As I've said in the comments if you have a grid with intensities why not fit density of bivariate distribution?

Here is the sample graph to illustrate my point:

Each grid point with is displayed as a square, colored according to intensity. Superimposed on the graph is the contour plot of bivariate normal density plot. As you can see the contour lines expand in the direction of decreasing intensity. The center will be controled by the mean of bivariate normal and the spread of the intensity according to covariance matrix.

To get the estimates of mean and covariance matrix simple numerical optimisation can be used, compare the intensities with values of density function using the mean and the covariance matrix as parameters. Minimize to get the estimates.

This is of course strictly speaking not a statistical estimate, but at least it will give you an idea how to proceed further.

Here is the code for reproducing the graph:

require(mvtnorm)
sigma=cbind(c(0.1,0.7*0.1),c(0.7*0.1,0.1))

x<-seq(0,1,by=0.01)
y<-seq(0,1,by=0.01)
z<-outer(x,y,function(x,y)dmvnorm(cbind(x,y),mean=mean,sigma=sigma))

mz<-melt(z)

mz$X1<-(mz$X1-1)/100
mz$X2<-(mz$X2-1)/100

colnames(mz)<-c("x","y","z")

mz$intensity<-round(mz$z*1000)

ggplot(mz, aes(x,y)) + geom_tile(aes(fill = intensity), colour = "white") + scale_fill_gradient(low = "white",     high = "steelblue")+geom_contour(aes(z=z),colour="black")

Answer 3

Your model is a two-dimensional random field $X[i,j]$, and you are trying to estimate the joint distribution of the integer-values random variables $X[i,j]$. You will want to assume spatial stationarity: that is, the joint distribution of $(X[i_1,j_1],...,X[i_m,j_m])$ is the same as the joint distribution of $(X[i_1+k,j_1+l]...,X[i_m+k,j_m+l])$. In particular, the marginal distribution is the same for every cell. A simple question to ask is the autocorrelation structure of the field. That is, what is $corr(X[i_1,j_1],X[i_2,j_2])$ given the distance $d([i_1,j_1],[i_2,j_2])$? We represent this as a function $\rho(d)$. A simple model for the autocorrelation structure is $\rho(d)=kd^{-1}$, where $k$ is a constant.

A 'gaussian' effect corresponds to a quadratic distance function, but there are many other distance functions you should consider, such as the taxicab norm $d([i_1,j_1],[i_2,j_2]) = |i_1-i_2|+|j_1-j_2|$. Once you have decided on a distance function and the form of your model for autocorrelation it is simple enough to estimate $\rho(d)$ e.g. via maximum likelihood. For more ideas, look for "random field".