I'm aware that the t-test needs 'normally distributed data'.
But take the variable y. When it is plotted without being split by group, it isn't normally distributed:
set.seed(1)
y <- c(rnorm(1000, 1), rnorm(1000, 5))
group <- c(rep("A", 1000), rep("B", 1000))
df <- data.frame(y=y, group=group)
library(ggplot2)
ggplot(df, aes(y)) + geom_histogram()
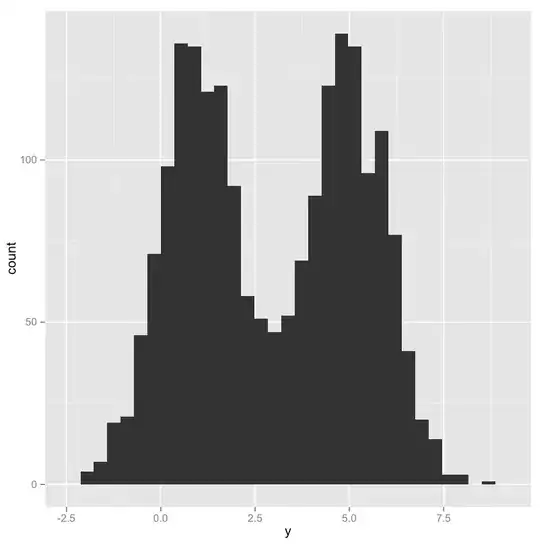
But when y is split by group, it is normally distributed:
ggplot(df, aes(y)) + geom_histogram() + facet_grid(~group)
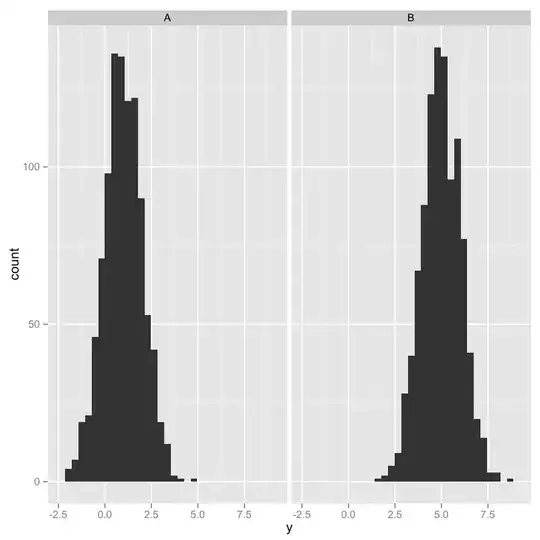
Can anyone clarify if a variable only needs to be normally distributed after being split by group?