I originally posted this as an answer elsewhere but in retrospect it seems more like a question: What is the sample-size range for which the median should be preferred to the mean as a measure of central tendency? And why?
I have R code that simulated neuron activity based on the model described at these links: http://www.izhikevich.org/publications/spikes.htm
http://www.izhikevich.org/publications/spikes.pdf
I know how to simulate one but not fit the parameters to existing data. Take this pattern which was generated with the code below. Each neuron could have different a, b, c, d, k1, k2, k3 parameters and also the I parameter (Input Current) could vary over time or be constant for each neuron. The model is described in the pdf above. Anyone know how to fit this model using R? What I would like to be able to do is fit a set of parameters to actual firing data (which would be voltage over time, same as what is simulated).
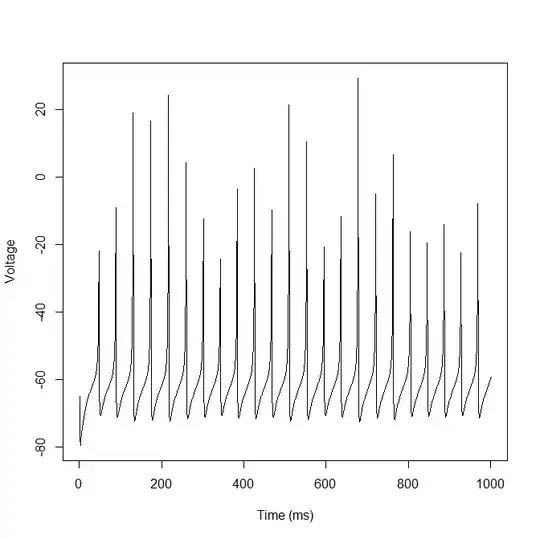
R code to simulate Neuron:
a=.1; b=.2; c=-65; d=2
k1=.04; k2=5; k3=140
I=4
Ntime=1000
v<-matrix(nrow=Ntime)
u<-matrix(nrow=Ntime)
v[1]=-65
u[1]=0
for(i in 1:Ntime){
#Fire Neuron if Voltage>30
if(v[i]>=30){
v[i]<-c
u[i]<-u[i]+d
}
#Calculate Voltage Change
dv= k1*v[i]^2 + k2*v[i] + k3 - u[i] + I
du= a*(b*v[i] -u[i])
#Update Voltage
v[i+1]<-v[i]+dv
u[i+1]<-u[i]+du
}
plot(v, type="l", xlab="Time (ms)", ylab="Voltage")