Suppose $X_1,\ldots,X_n$ are random samples of a $U(0,\theta)$ distribution. If $Y_n$ are the largest order statistics of the sample, and $V=\displaystyle\frac{n\bar{X}}{Y_n}$, how can I calculate the probability density function of $V$?
-
Duplicate of: http://math.stackexchange.com/questions/731089/calculating-var3t-y-n-in-uniform-distribution#comment1526812_731089 – wolfies Apr 01 '14 at 06:43
-
Duplicate of: http://stats.stackexchange.com/questions/91801/finding-var3t-y-n-in-uniform-distribution – wolfies Apr 01 '14 at 06:44
-
Duplicate of: http://stats.stackexchange.com/questions/91961/joint-distribution-of-a-random-variable-and-the-sample-maximum – wolfies Apr 01 '14 at 06:47
-
1Definitely *not* a duplicate of 91961, because the joint distribution of $(X_1, Y_n)$ gives little information about $V$. – whuber Apr 01 '14 at 14:35
1 Answers
Let the order statistics be $X_{[1]}\le X_{[2]}\le\cdots\le X_{[n]}$ and assume the $\{X_i\}$ are independent. The following are well known:
The joint distribution of the order statistics $(X_{[i]})$ is uniform on the set $0\le X_{[1]}\le X_{[2]}\le\cdots\le X_{[n]}\le \theta.$ This is a consequence of (a) the uniformity of $(X_1,X_2,\ldots, X_n)$ and (b) the map that takes $(X_1, X_2, \ldots, X_n)$ into its sorted version (the order statistics) is an $n!$ to $1$ probability-preserving map. Thus the joint pdf of the order statistics is
$$f_\theta(y_1,y_2, \ldots, y_n) = \frac{n!}{\theta^n}I(0\le y_1\le y_2\le \cdots \le y_n \le \theta)$$
($I$ is the indicator function).
The marginal CDF of the maximum, $X_{[n]}$, is
$$F_n(y_n) = {\Pr}_\theta(X_{[n]}\le y_n) = {\Pr}_\theta(X_1\le y_n)\cdots{\Pr}_\theta(X_n\le y_n) = \left(\frac{y_n}{\theta}\right)^n$$
whence its PDF is
$$f_n(y_n) = \frac{d F_n(y_n)}{d y_n} = \frac{n y_n^{n-1}}{\theta^n}.$$
Dividing $f_\theta$ by $f_n$ shows the conditional distribution of the sum
$$Y = X_{[1]}+\cdots X_{[n-1]} = X_1+X_2+\cdots+X_n - X_{[n]} = n\bar{X}-X_{[n]}$$
is
$$f_Y(y\ |\ X_{[n]}=y_n) = \frac{(n-1)!}{y_n^{n-1}}I(0\le y_1\le y_2\le \cdots \le y_{n-1} \le y_{n}).$$
This is recognizable (by comparing to result (1) above) as the distribution of the order statistics of $n-1$ iid uniform$(0, y_n)$ variates. Dividing by $y_n$ rescales them to iid uniform$(0,1)$ variates, whence the distribution of $\frac{Y}{X_{[n]}} = V-1$ is that of the sum of $n-1$ iid uniform$(0,1)$ variables. That distribution is described at elsewhere on our site at https://stats.stackexchange.com/a/43075, which gives four ways to derive its PDF.
An R simulation bears out this result. The output plots compare histograms of $V$ to its PDF (overdrawn in red); the match is excellent:
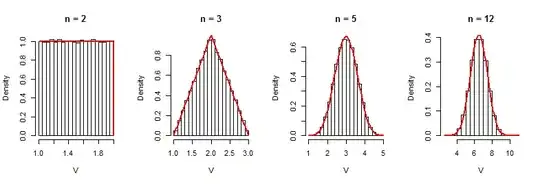
#
# Compute the PDF of a sum of `n` iid uniform(0,1) variables.
#
unif.sum <- function(x, n) {
theta <- function(y) ifelse(y >= 0, y^(n-1), 0)
s <- outer(0:n, x, function(i, y) choose(n, i)*theta(y-i)*(-1)^i)
apply(s, 2, sum) / factorial(n-1)
}
#
# Simulate V for various values of `n` and visually compare to the
# theoretically derived PDF.
#
n.iter <- 10^5 # Number of samples per simulation
ns <- c(2, 3, 5, 12) # Sample sizes to investigate
par(mfrow=c(1,length(ns))) # Display all plots in a row
for(n in ns) {
V <- t(apply(matrix(runif(n*n.iter), ncol=n), 1, function(y) sum(y)/max(y)))
hist(V, main=paste("n =", n), freq=FALSE)
curve(unif.sum(x-1, n-1), col="Red", lwd=2, add=TRUE)
}
-
Nice answer. But given that the same question has been posed by 3 different people (or 3 different names) on 2 different sites ... it seems you are probably doing their homework for them, which may not be a good thing. One can only hope that this arrived too late to be used in their assignment :) – wolfies Apr 02 '14 at 07:42
-
@wolfies This doesn't look like homework to me (for several reasons, including that the various questions reflect efforts to attack and simplify the problem). Regardless, *we shouldn't care whether problems are homework.* Policing student honesty is not our task. What matters for us are the nature and quality of the question: when a question is so obviously of a routine textbook nature we treat it a little differently than others. Although there's no clear dividing line between routine and non-routine, this one strikes me as being on the answerable side of that line. – whuber Apr 02 '14 at 17:12