8

Concerning the Pearson chi-square test there seems to be a subtle difference between the goodness-of-fit test and the test of independence.

What is confusing is that both tests seem to be calculated in a very similar way.

My question: What is the real difference and how to handle that in practice?

(NB: This is question is related, yet not the same: Test of independence vs test of homogeneity)

Community
  • 1
vonjd
  • 5,886
  • 4
  • 47
  • 59

3 Answers3

6

1) A goodness of fit test is for testing whether a set of multinomial counts is distributed according to a prespecified (i.e. before you see the data!) set of population proportions.

2) A test of homogeneity tests whether two (or more) sets of multinomial counts come from different sets of population proportions.

3) A test of independence tests is for a bivariate** multinomial, of whether $p_{ij}$ is different from $p_{i}\,p_{j}$.

**(usually)

Sometimes people make the mistake of treating the second case as if it were the first. This underestimates the variability between the proportions. (If one sample is very large the error in treating it as population proportions will be relatively small.)

Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • To add a small point to this great answer, a goodness of fit test can also be performed after you've seen the data/with parameters unknown but estimated using, for example, MLE. If performing the goodness of fit test with parameters unknown, then you'd use MLE estimated probabilities in the observed Pearson d1 statistic, and its number of degrees of freedom would be reduced by the number of estimated parameters. Everything else is same as in the case when the parameters are known/before you see the data. – ColorStatistics Apr 10 '20 at 00:01
  • This is correct as stated - and an important point to add - but perhaps I should be explicit that this accounting for loss of df with parameters estimated by MLE is only the case if the MLE is performed on the multinomial counts rather than on unbinned data (e.g. if you're trying to test some continuous distribution fit by binning the data, the loss of d.f. in the chi-squared approximation rely on that estimation being done with the binned data). – Glen_b Apr 10 '20 at 03:25
0

There are 2 primary differences between a Pearson goodness of fit test and a Pearson test of independence:

  1. The test of independence presumes that you have 2 random variables and you want to test their independence given the sample at hand. The goodness of fit test, on the other hand, works on 1 random variable at a time. You can test whether the Pearson d statistic is large enough to reject the null hypothesis that your sample came from the hypothesized distribution. You can do so a) if all parameters are known or b) if parameters are unknown and need to be estimated (using MLE for example). In the latter case, the number of degrees of freedom of the Pearson d statistic is reduced by the number of estimated parameters.
  2. But the key difference, in my mind, between the goodness of fit test and the test of independence is the assumption under which the expected counts are calculated. In the case of goodness of fit, the expected counts are calculated under the assumption that the sample came from the hypothesized distribution. In the case of the test of independence, the expected counts are calculated under the assumption that the 2 random variables are independent, as follows. Suppose you have random variables A and B, each partitioned as depicted in the table of observed counts below.

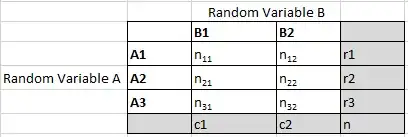
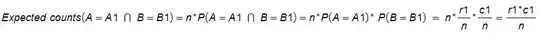enter image description here

To calculate the expected counts for the first cell:

enter image description here

ColorStatistics
  • 2,699
  • 1
  • 10
  • 26
0

You may want to calculate the independence between two variables, A and B (test of independence) or if the distribution of A given B=B1 (first column) fits the distribution of A given B=B2 (second column). That is if P(A|B=B1)=P(A|B=B2). I'm taking as example the data table posted by @ColorStatistics in her answer.

The two calculations are slightly different, the test of independence takes into account the differences of both distributions with the expected counts, so you have more terms but smaller (the expected counts are "in between" the observed values), the goodness of fit test takes into account the differences of the first distribution from the other (the expected counts are the values of the second distribution), so you have less terms but bigger.

The two methods tend to be same if one subtotal of B is much greater than the other and accounts for most of the elements, that is the B2 elements are very slightly influenced by the exctraction of the B1 elements (c2>>c1 and c2~N). In this case the expected counts for the B2 column are almost equal to their values. So computing the difference with the expected counts (test of independence) is almost the same as computing the difference with the B2 column (goodness of fit test).

Luke
  • 135
  • 6