Switchpoint detection with probabilistic programming (pymc)

Question

I'm currently reading the Probabilistic Programming and Bayesian Methods for Hackers "book". I've read a few chapters and I was thinking on the first Chapter where the first example with pymc consist of detecting a witchpoint in text messages. In that example the random variable to indicate when the switchpoint is happening is indicated with $\tau$. After the MCMC step the posterior distribution of $\tau$ is given: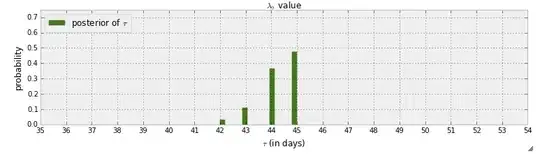

Firstly what can be learned from this graph is that there is a propability of almost 50% that the switchpoint happend on day 45. Though what if there wasn't a switchpoint ? Instead of assuming there is a switchpoint and then trying to find it, I want to detect if there is in fact a switchpoint.

The author answers the question "did a switchpoint happen" by "Had no change occurred, or had the change been gradual over time, the posterior distribution of $\tau$ would have been more spread out". But how can you answer this with a propability, for example there is a 90% chance a switchpoint happend, and there is a 50% chance it happend on day 45.

Does the model need to be changed ? Or can this be answered with the current model ?

Answer 1

SeanEaster has some good advice. Bayes factor can be difficult to compute, but there are some good blog posts specifically for Bayes factor in PyMC2.

A closly related question is goodness-of-fit of a model. A fair method for this is just inspection - posteriors can give us evidence of goodness-of-fit. Like quoted:

"Had no change occurred, or had the change been gradual over time, the posterior distribution of $\tau$ would have been more spread out"

This is true. The posterior is quite peaked near time 45. As you say > 50% of the mass is at 45, whereas if there was no switch point the mass should (theoretically) be closer to 1/80 = 1.125% at time 45.

What you are aiming to do is faithfully reconstruct the observed data set, given your model. In Chapter 2, their are simulations of generating fake data. If your observed data looks wildly different from your artificial data, then likely your model is not the correct fit.

I apologize for the non-rigourous answer, but really it's a major difficulty that I haven't efficiently overcome.

Answer 2

That's more of a model comparison question: The interest is in whether a model without a switchpoint better explains the data than a model with a switchpoint. One approach to answer that question is to compute the Bayes factor of models with and without a switchpoint. In short, the Bayes factor is the ratio of probabilities of the data under both models:

$K = \frac{\Pr(D|M_1)}{\Pr(D|M_2)} =\frac{\int\Pr(\theta_1|M_1)\Pr(D|\theta_1,M_1)\,d\theta_1}{\int \Pr(\theta_2|M_2)\Pr(D|\theta_2,M_2)\,d\theta_2}$

If $M_1$ is the model using a switchpoint, and $M_2$ is the model without, then a high value for $K$ can be interpreted as strongly favoring the switchpoint model. (The wikipedia article linked above gives guidelines for what K values are noteworthy.)

Also note that in an MCMC context the above integrals would be replaced with sums of parameter values from the MCMC chains. A more thorough treatment of Bayes factors, with examples, is available here.

To the question of computing the probability of a switchpoint, that's equivalent to solving for $P(M_1|D)$. If you assume equal priors across the two models, then the posterior odds of the models are equivalent to the Bayes factor. (See slide 5 here.) Then it's just a matter of solving for $P(M_1|D)$ using the Bayes factor and the requirement that $\sum\limits_{i=1}^n P(M_i|D) = 1$ for n (exclusive) model events under consideration.