I have four relatively small sets of data under five different conditions. For each set of data I want to see whether the differences between the conditions are statistically significant. The first two sets are by visual inspection (histograms) the least normally distributed, whereas the two latter sets look almost normally distributed, with a few peaks outside what would be the Gaussian function. All data sets fail Kolmogorov-Smirnov and the t-test, but succeed the Chi-square goodness of fit test. The quantile-quantile plot for the first and last set is plotted below, which also suggests almost normal distribution for the better sets (is linear enough, or must it be 45 degrees?):
set1:
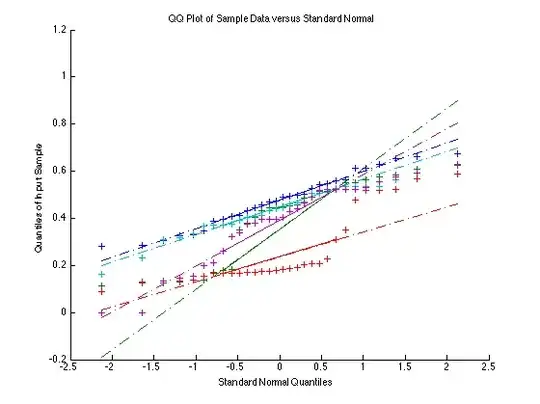
set 4:
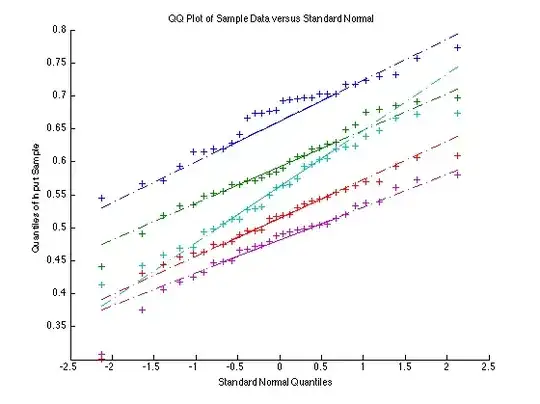
The p-values for an ANOVA and Kruskal-Wallis for the four data sets are:
ANOVA Kruskal Wallis
set 1 3.21e-07 5.31-05
set 2 1.23e-06 1.04e-04
set 3 3.39e-11 1.18e-16
set 4 1.31e-23 7.20e-17
The outcome of those tests indicate what I found by visual inspection, that the sets are more and more normally distributed from set 1 to set 4. However, in other research and examples I generally see p-values in e.g. ~0.00X. These values are tiny! It seems counter-intuitive given that the data sets failed tests for normality. Is that a reason for concern? Given these results, am I justified in running the ANOVA and plotting confidence intervals, regardless of the fact that the t-test and Kolmogorov-Smirnov test failed? I know that the ANOVA is relatively robust towards non-normal distributions, but is my data too far off?
Edit: Results of t-tests for first and last set as requested:
t-test:
set 1
condition 1 2 3 4 5
H 1 1 1 1 1
P (1e-09 *) 0.0000 0.0007 0.5115 0.0000 0.0007
set 4
condition 1 2 3 4 5
H 1 1 1 1 1
P (1e-11 *) 0.0000 0.0000 0.0000 0.1729 0.0000