I was trying to derive the equations from page 109 in "elements of statistical learning" (image below)
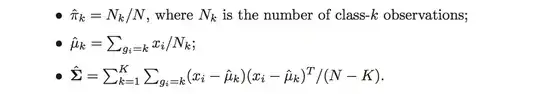
To be honest, I am not sure how the covariance $\Sigma$ is estimated (the third bullet point in image). Can someone kindly show me and how $\hat{\Sigma}$ is derived (in particular I am not sure how $N - K$ appear in the denominator) ? Thanks
UPDATE: I still cannot figure why $N-K$ (where $K$ is the number of parameters) shows up in the denominator, but I suspect it has to do with making the covariance matrix estimator unbiased. This is similar to $\frac{1}{N} \sum_i (x_i - \bar{x})^2$ is biased, while $s^2 = \frac{1}{N-1} \sum_i (x_i - \bar{x})^2$ is not. Please CORRECT ME IF I AM WRONG.