According to the Wikipedia article, we have the scenario shown below, but how can ABC generate simulation datasets from samples of $\theta$ without knowing or evaluating the likelihood function?
For example, how would this method work for a normal $N(\mu, \sigma)$ distribution? Assuming that the parameter to estimate is $\mu$ and that $\sigma$ is known, how would it generate the simulations without evaluating $N(\mu, \sigma)$?
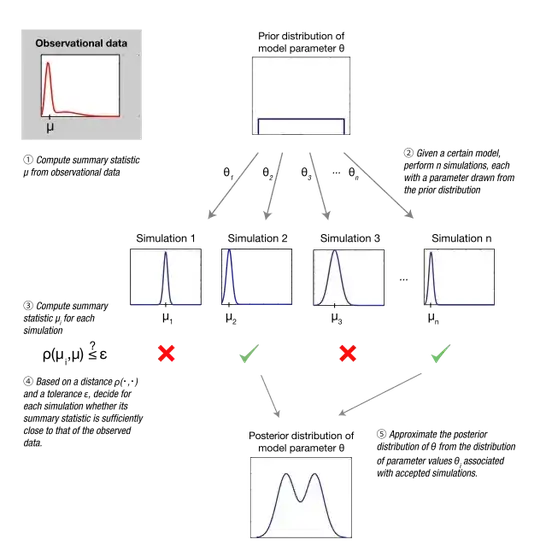
Approximate Bayesian Computation (ABC) is useful when you can simulate data, but cannot evaluate the likelihood function analytically. You seem to assume that it is necessary to know the likelihood function $l(\theta) = P[D|\theta]$ to simulate data. I'm not sure how you came to that conclusion, but there are ways to simulate data that do not involve the likelihood. ABC does not 'provide' you with such a way of simulating data. You have to come up with some suitable simulation approach yourself.
In your example, one would draw values for $\mu$ from the prior distribution $p(\theta)$, and simulate a sample $\tilde D$ from an $N(\mu, \sigma)$ distribution. We can use a quantile-transformation $\Phi^{-1}(u)$ of a uniform distributed random number $u$ here. This requires that we know the quantile-function $\Phi^{-1}$ of $N(\mu, \sigma)$, but not the likelihood function $P[D|\theta]$. Alternative, we could even do a real world experiment which is known to produce $N(\mu,\sigma)$ disturbed measurements.
The idea of ABC now is, that if $\tilde D$ is identical to the real data $D$, then $\theta$ also is a sample from the posterior distribution $p(\theta|D)$. If we get enough of such samples, we can use the then to approximate the posterior distribution itself. As we normally would hardly ever observe a simulation with produces exactly $D$, we allow for a small mismatch $\epsilon$ between $D$ and $\tilde D$, which introduces another approximation.
