14

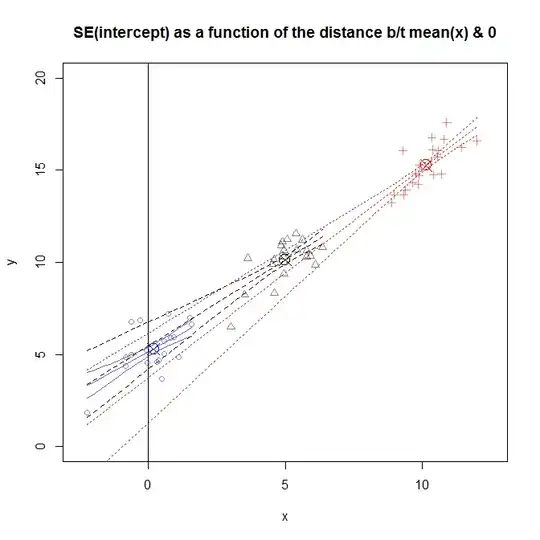
The standard error of the intercept term ($\hat{\beta}_0$) in $y=\beta_1x+\beta_0+\varepsilon$ is given by $$SE(\hat{\beta}_0)^2 = \sigma^2\left[\frac{1}{n}+\frac{\bar{x}^2}{\sum_{i=1}^n(x_i-\bar{x})^2}\right]$$ where $\bar{x}$ is the mean of the $x_i$'s.

From what I understand, the SE quantifies your uncertainty- for instance, in 95% of the samples, the interval $[\hat{\beta}_0-2SE,\hat{\beta}_0+2SE]$ will contain the true $\beta_0$. I fail to understand how the SE, a measure of uncertainty, increases with $\bar{x}$. If I simply shift my data, so that $\bar{x}=0$, my uncertainty goes down? That seems unreasonable.

An analogous interpretation is - in the uncentered version of my data, $\hat{\beta}_0$ corresponds to my prediction at $x=0$, while in the centered data, $\hat{\beta}_0$ corresponds to my prediction at $x=\bar{x}$. So does this then mean that my uncertainty about my prediction at $x=0$ is greater than my uncertainty about my prediction at $x=\bar{x}$? That seems unreasonable too, the error $\epsilon$ has the same variance for all values of $x$, so my uncertainty in my predicted values should be the same for all $x$.

There are gaps in my understanding I'm sure. Could somebody help me understand what's going on?

gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
elexhobby
  • 775
  • 1
  • 5
  • 16
  • 4
    Have you ever regressed anything against a date? Many computer systems start their dates in the distant past, often over 100 or over 2000 years ago. The intercept estimates the value of your data *extrapolated backwards* to that starting time. How certain would you be, say, of the gross domestic product of Iraq in the year 0 CE based on regressing a series of 21st century data? – whuber Mar 12 '14 at 19:30
  • I agree, it makes sense if you think about it this way. This, and gung's answer, make things clear. – elexhobby Mar 12 '14 at 19:45
  • 3
    [This answer](http://stats.stackexchange.com/questions/85560/shape-of-confidence-interval-for-predicted-values-in-linear-regression/85565#85565) gives an intuitive explanation, with diagrams) of how it arises, by casting the fitted line in terms of the fit at the mean $\bar x$ (the fitted line passes through $(\bar x,\bar y)$) and shows why the position of where the line can go spreads out as you move away from $\bar x$ (which is caused by the uncertainty in the slope). – Glen_b Mar 12 '14 at 21:52

1 Answers1

16

Because the regression line fit by ordinary least squares will necessarily go through the mean of your data (i.e., $(\bar x, \bar y)$)—at least as long as you don't suppress the intercept—uncertainty about the true value of the slope has no effect on the vertical position of the line at the mean of $x$ (i.e., at $\hat y_{\bar x}$). This translates into less vertical uncertainty at $\bar x$ than you have the further away from $\bar x$ you are. If the intercept, where $x=0$ is $\bar x$, then this will minimize your uncertainty about the true value of $\beta_0$. In mathematical terms, this translates into the smallest possible value of the standard error for $\hat\beta_0$.

Here is a quick example in R: 

set.seed(1)                           # this makes the example exactly reproducible
x0      = rnorm(20, mean=0, sd=1)     # the mean of x varies from 0 to 10
x5      = rnorm(20, mean=5, sd=1)
x10     = rnorm(20, mean=10, sd=1)
y0      = 5 + 1*x0  + rnorm(20)       # all data come from the same  
y5      = 5 + 1*x5  + rnorm(20)       #  data generating process
y10     = 5 + 1*x10 + rnorm(20)
model0  = lm(y0~x0)                   # all models are fit the same way
model5  = lm(y5~x5)
model10 = lm(y10~x10)

enter image description here

This figure is a bit busy, but you can see the data from several different studies where the distribution of $x$ was closer or further from $0$. The slopes differ a little from study to study, but are largely similar. (Notice they all go through the circled X that I used to mark $(\bar x, \bar y)$.) Nonetheless, the uncertainty about the true value of those slopes causes the uncertainty about $\hat y$ to expand the further you get from $\bar x$, meaning that the $SE(\hat\beta_0)$ is very wide for the data that were sampled in the neighborhood of $x=10$, and very narrow for the study in which the data were sampled near $x=0$.

Edit in response to comment: Unfortunately, centering your data after you have them will not help you if you want to know the likely $y$ value at some $x$ value $x_\text{new}$. Instead, you need to center your data collection on the point you care about in the first place. To understand these issues more fully, it may help you to read my answer here: Linear regression prediction interval.

gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
  • So, lets say for some reason I'm most interested in the prediction at the value $x=x'$. The above explanation implies that I shouldn't center my data (i.e. shift $x$ so that $\bar{x}=0$), but instead shift it so that $\bar{x}=x'$. Is this correct? – elexhobby Mar 12 '14 at 19:48
  • The general formula has $(x^\prime - \bar{x})^2$ in the numerator instead of $\bar{x}^2$: no shifting is needed. – whuber Mar 12 '14 at 20:27
  • @elexhobby, I added some info to answer your comment, you might also want to look at the linked material. Let me know if you still need more. – gung - Reinstate Monica Mar 12 '14 at 20:48
  • Here's how I understand - I read elsewhere that $SE(\hat{\beta}_1)=\frac{\sigma^2}{\sum(x_i-\bar{x})^2}$. Now the error in the predicted value at $x_{new}$ due to this uncertainty in the slope is $SE(\hat{\beta}_1)(x_{new}-\bar{x})^2$. Furthermore, the error due to uncertainty in the vertical position of the line is $\frac{\sigma^2}{n}$. Combine these together, and we get the uncertainty in the predicted value due to uncertainty in $\hat{\beta}_1$ and $\hat{\beta}_0$ is $\frac{\sigma^2}{n}+\frac{\sigma^2(x_{new}-\bar{x})^2}{\sum(x_i-\bar{x})^2}$. Correct me if I'm wrong. – elexhobby Mar 13 '14 at 04:44
  • 1
    Furthermore, it is clear why the error in the vertical position is $\frac{\sigma^2}{n}$ - we know that the line has to pass through $\bar{y}$ at $x=\bar{x}$. Now $\bar{y}$ contains the average of $n$ iid errors, and hence will have SE equal to $\frac{\sigma^2}{n}$. Wow! Thanks a lot for your diagram and clear explanation, I really appreciate. – elexhobby Mar 13 '14 at 04:57
  • It sounds like you have it, @elexhobby. – gung - Reinstate Monica Mar 13 '14 at 13:45