2

I am working on a dataset that ranges between 0 - 100 and typically is centered around 50 for the most part. It seems like the dataset shows a triangular distribution given its bound between 0 - 100. I wasn't sure and just wanted to double check if this would be a triangular distribution?

Can we compute z-score for this dataset? If not how would you recommend analyzing this dataset on a cross-sectional as well as time series basis?

Glen_b
  • 257,508
  • 32
  • 553
  • 939
user40678
  • 21
  • 1
  • 2
    I don't think there's enough information to answer any of the questions here, apart from the 'Can we compute a z-score' one (obviously you can *compute* a z-score, you just need a mean and standard deviation to standardize it with). – Glen_b Mar 04 '14 at 04:59
  • To make the intent of my previous comment a little more explicit, please edit your question to explain in much more detail (preferably with pictures where possible). I think there may be some useful points to be made. (Do you only have the one variable? When you say it's cross sectional as well as time series, can you explain more about what you have?) – Glen_b Mar 04 '14 at 07:25

1 Answers1

2

Your description is insufficient basis for identifying the distribution. Several distributions can fit your description (e.g., a truncated normal distribution). Wikipedia defines triangular distributions by further conditions. In your case, if your distribution's mode $=50$, the triangular would be: $PDF= \begin{cases} 0 & \mathrm{for\ } x < 0, \\ \frac{x}{2500} & \mathrm{for\ } 0 \le x \leq 50, \\[4pt] \frac{100-x}{2500} & \mathrm{for\ } 50 < x \le 100, \\[4pt] 0 & \mathrm{for\ } 100 < x \end{cases}$

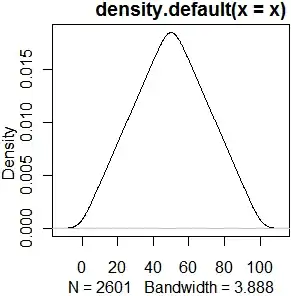
If that's not exactly what your distribution looks like (assuming the mode is exactly 50, which it doesn't need to be; the distribution can be asymmetric around an off-center mode), then it's not exactly triangular. It might be approximately triangular, but then it might also be considered approximately normal. After all, skewness $= 0$ and kurtosis $=-.6$ for an exactly (symmetric) triangular distribution, which isn't too bad. Regarding what's "approximate enough" for your intended purposes, I recommend reading, "Is normality testing 'essentially useless'?" It's a good primer on graphical analysis and interpretation for distribution identification. Another useful point therein: the sensitivity of an analysis to distributional assumptions depends on what analysis we're talking about (and you haven't specified that either).

Technically, if your dataset is a , and if you don't know the 's $\mu$ and $\sigma$, you can only calculate $t$-statistics $(\frac{x-\bar X}s)$ where $\bar X$ and $s$ are the sample mean and $SD$, respectively, because $z$-scores are defined in terms of population s. But now I'm being more technical than @Glen_b, so you can probably ignore this detail quite safely!

Community
  • 1
Nick Stauner
  • 11,558
  • 5
  • 47
  • 105
  • Did I just get called 'technical'? If so, I'd take it as a compliment. I tend to feel myself to be a pretty basic, applied sort of fellow. I do hope the OP edits to include more information; I find the triangular distribution a fun object to play with. – Glen_b Mar 04 '14 at 07:19
  • Haha...You may be right about yourself overall, but you're surely more technically savvy than me! My point is that if you think, "Obviously you can *compute* a z-score," then my point about the difference between $t$-statistics and $z$-scores must be pretty negligible, because I expect you would note the difference if it were ever really going to matter. I didn't even know there was a difference until I checked Wikipedia a few hours ago! – Nick Stauner Mar 04 '14 at 07:27