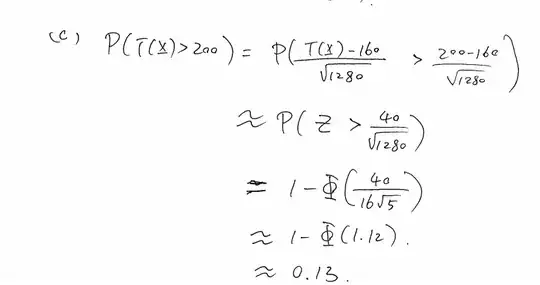Suppose $X_1,...,X_n$ are iid from $N(\mu,\sigma^2)$, how can I find $P(T(X)>200)$?

Question

Suppose $X_1,...,X_n$ are iid from $N(\mu,\sigma^2)$ with $\mu$ unknown and $\sigma = 2$ known. Letting $T(X) = \sum{(X_i-\mu)^2}$ from i = 1 to 40, how can I use the central limit theorem to approximate $P(T(X)>200)$?

I found that $E(T(X))=40$ and $Var(T(X))=160$ and $T(X)$ ~ Chi square with n=40 df.

The below is the correct answer, but I do not know how this makes sense since my understanding of the central limit theorem is that the average of iid random variables is normal, but how am I utilizing the central limit below? Thanks!!!!

Answer 1

Try letting $Y_i = (X_i - \mu)^2$ for $i = 1,\ldots, 40$. Then what are $E(Y_i)$ and Var$(Y_i)$ equal to? You should be able to work it out using the CLT from there. Also, note that $T(X)$ does not have a Chi-Square distribution with 40 degrees of freedom. But $T(X)/4$ does since it is the sum of squares of Standard independent normal random variables.

Answer 2

As described in the answer pointed to by a comment on the question, the Central Limit Theorem examines sums of random variables from which we subtract the mean of the sum and then divide the whole by the standard deviation of the sum: let $Y_1,...,Y_n$ be random variables and define $S_n \equiv \sum_{i=1}^nY_i$. Then the CLT examines the random variable

$$Z_n = \frac {S_n - E[S_n]}{\sqrt {\text {Var}(S_n)}}$$

In its most basic variant, the $Y_i$'s are identically and independently distributed, with existing / finite moments. In such a case, with common mean $\mu$ and common variance $\sigma^2$ we have $$Z_n = \frac {S_n - n\mu}{\sigma\sqrt n }$$

Given its conditions (which are usually sufficient but not necessary), the CLT asserts that $Z_n \rightarrow_d N(0,1)$ and therefore it provides a result related to the limiting distribution function of $Z_n$ as $n$ goes very-very far away.

So in order to have the "right" to apply the CLT in your case, you have first to show that you do have a $Z_n$-variable to deal with, and that this variable satisfies the conditions that are sufficient for the CLT (or that it does not satisfy the sufficient conditions but nevertheless obeys the CLT -there are such cases).
So define the random variable

$$Y_i = \frac {X_i-\mu}{\sigma} \sim N(0,1) \Rightarrow Y_i^2 \sim \chi^2(1)$$ with $E(Y_i^2) =1$ and $\text{Var}(Y_i^2) =2$. So a "$Z_n$" variable here would be

$$Z_n = \frac {\sum_{i=1}^{n}Y_i^2 - n}{\sqrt{2n}} = \frac {T(X) - n\sigma^2}{\sigma^2\sqrt{2n}}$$

and using $\sigma^2 = 4$ we get

$$Z_n = \frac {T(X) - 4n}{4\sqrt{2n}} $$

You should verify that the CLT applies for this $Z_n$ variable (it does). Therefore

$$\frac {T(X) - 4n}{4\sqrt{2n}} = Z_n \rightarrow_d N(0,1)$$

The approximation comes now and consists in "ignoring" that the above distributional result holds asymptotically (i.e. for $n\rightarrow \infty$), and using it for finite $n$. In your case $n = 40$, plug it in and get your results.

ADDENDUM
Responding to a comment, note that $X_i-\mu \sim N(0,\sigma^2)$ and so $(X_i-\mu)^2 \sim \text{Gamma}(1/2, 2\sigma^2)$ and so $T(X) \sim \text{Gamma}(n/2, 2\sigma^2)$ exactly. Then one can calculate the desired probability by inserting the value $200$ in the Survival function of the $\text{Gamma}(20, 8)$ distribution (shape-scale parametrization).