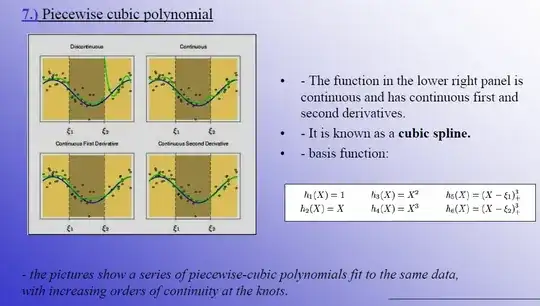
I am trying to wrap my head around splines and the concept of basis functions using the Elements of Statistical Learning. I understand that the goal is to find polynomials that are continuous at first and second derivatives. However, following the picture below, I don't understand whether
- a) the spline consists of a different cubic function $(a+bx+cx^2+dx^3)$ in each of the three regions, or
- b) whether the spline is the linear addition of the 6 basis functions per below across the entire domain, or
- c) whether there are 6 basis functions with different parameters in each of the 3 regions (hence 18 different functions). Much appreciated...