11

I'm working on a classification problem that computes a similarity metric between two input x-ray images. If the images are of the same person (label of 'right'), a higher metric will be calculated; input images of two different people (label of 'wrong') will result in a lower metric.

I used a stratified 10-fold cross-validation to calculate the misclassification probability. My current sample size is around 40 right matches and 80 wrong matches, where each datapoint is the calculated metric. I'm getting a misclassification probability of 0.00, but I need some sort of confidence interval / error analysis on this.

I was looking into using a binomial proportion confidence interval (where I'd use the results of the cross-validation as a correct labeling or incorrect labeling for my number of successes). However, one of the assumptions behind the binomial analysis is the same probability of success for each trial, and I'm not sure if the method behind the classification of 'right' or 'wrong' in the cross-validation can be considered to have the same probability of success.

The only other analysis I can think of is to repeat the cross-validation X times and calculate the mean/standard deviation of the classification error, but I'm not sure if this is even appropriate as I'd be reusing the data from my relatively small sample size several times.

Any thoughts? I'm using MATLAB for all my analysis, and I do have the Statistics toolbox. Would appreciate any and all assistance!

amoeba
  • 93,463
  • 28
  • 275
  • 317
Sean
  • 113
  • 1
  • 8
  • Misclassification probability of 0.00 means that you get 100% classification accuracy on each of the 10 cross-validation folds? – amoeba Feb 27 '14 at 20:45
  • Yes, this is correct. Each of the folds resulted in no misclassifications; the 0.00 I reported represents the total number of misclassifications (0) out of the total number of test cases (120). – Sean Feb 27 '14 at 21:16
  • BTW, what exactly do you mean by "stratified" cross-validation? On each CV fold you have 120/10=12 test samples, with always 4 matches and 8 non-matches? – amoeba Feb 27 '14 at 22:15
  • Yep, that's exactly it -- at least that's the way I understand how it's being done within MATLAB. Each fold should contain the same proportion of the 'right' / 'wrong' class labels, which is 1:2. – Sean Feb 27 '14 at 23:44

3 Answers3

7

Influence of instability in the predictions of different surrogate models

However, one of the assumptions behind the binomial analysis is the same probability of success for each trial, and I'm not sure if the method behind the classification of 'right' or 'wrong' in the cross-validation can be considered to have the same probability of success.

Well, usually that equvalence is an assumption that is also needed to allow you to pool the results of the different surrogate models.

In practice, your intuition that this assumption may be violated is often true. But you can measure whether this is the case. That is where I find iterated cross validation helpful: The stability of predictions for the same case by different surrogate models lets you judge whether the models are equivalent (stable predictions) or not.

Here's a scheme of iterated (aka repeated) $k$-fold cross validation:
iterated k-fold cross validation

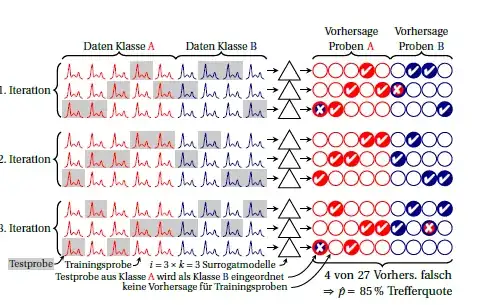
Classes are red and blue. The circles on the right symbolize the predictions. In each iteration, each sample is predicted exactly once. Usually, the grand mean is used as performance estimate, implicitly assuming that the performance of the $i \cdot k$ surrogate models is equal. If you look for each sample at the predictions made by different surrogate models (i.e. across the columns), you can see how stable the predictions are for this sample.

You can also calculate the performance for each iteration (block of 3 rows in the drawing). Any variance between these means that the assumption that surrogate models are equivalent (to each other and furthermore to the "grand model" built on all cases) is not met. But this also tells you how much instability you have. For the binomial proportion I think as long as the true performance is the same (i.e. independent whether always the same cases are wrongly predicted or whether the same number but different cases are wrongly predicted). I don't know whether one could sensibly assume a particular distribution for the performance of the surrogate models. But I think it is in any case an advantage over the currently common reporting of classification errors if you report that instability at all. I think you could report this variance and argue that as $k$ surrogate models were pooled already for each of the iterations, the instability variance is roughly $k$ times the observed variance between the iterations.

I usually have to work with far less than 120 independent cases, so I put very strong regularization on my models. I'm then usually able to show that the instability variance is $\ll$ than the finite test sample size variance. (And I think this is sensible for the modeling as humans are biased towards detecting patterns and thus drawn towards building too complex models and thus overfitting).
I usually report percentiles of the observed instability variance over the iterations (and $n$, $k$ and $i$) and binomial confidence intervals on the average observed performance for the finite test sample size.

The drawing is a newer version of fig. 5 in this paper: Beleites, C. & Salzer, R.: Assessing and improving the stability of chemometric models in small sample size situations, Anal Bioanal Chem, 390, 1261-1271 (2008). DOI: 10.1007/s00216-007-1818-6
Note that when we wrote the paper I had not yet fully realized the different sources of variance which I explained here - keep that in mind. I therefore think that the argumentation for effective sample size estimation given there is not correct, even though the application conclusion that different tissue types within each patient contribute about as much overall information as a new patient with a given tissue type is probably still valid (I have a totally different type of evidence which also points that way). However, I'm not yet completely sure about this (nor how to do it better and thus be able to check), and this issue is unrelated to your question.

Which performance to use for the binomial confidence interval?

So far, I've been using the average observed performance. You could also use the worst observed performance: the closer the observed performance is to 0.5, the larger the variance and thus the confidence interval. Thus, confidence intervals of the observed performance nearest to 0.5 give you some conservative "safety margin".

Note that some methods to calculate binomial confidence intervals work also if the observed number of successes is not an integer. I use the "integration of the Bayesian posterior probability" as described in
Ross, T. D.: Accurate confidence intervals for binomial proportion and Poisson rate estimation, Comput Biol Med, 33, 509-531 (2003). DOI: 10.1016/S0010-4825(03)00019-2

(I don't know for Matlab, but in R you can use binom::binom.bayes with both shape parameters set to 1).

These thoughts apply to predictions models built on this training data set yield for unknown new cases. If you need to generatlize to other training data sets drawn from the same population of cases, you'd need to estimate how much models trained on a new training samples of size $n$ vary. (I have no idea how to do that other than by getting "physically" new training data sets)

See also: Bengio, Y. and Grandvalet, Y.: No Unbiased Estimator of the Variance of K-Fold Cross-Validation, Journal of Machine Learning Research, 2004, 5, 1089-1105.

(Thinking more about these things is on my research todo-list..., but as I'm coming from experimental science I like to complement the theoretical and simulation conclusions with experimental data - which is difficult here as I'd need a large set of independent cases for reference testing)

Update: is it justified to assume a biomial distribution?

I see the k-fold CV a like the following coin-throwing experiment: instead of throwing one coin a large number of times, $k$ coins produced by the same machine are thrown a smaller number of times. In this picture, I think @Tal points out that the coins are not the same. Which is obviously true. I think what should and what can be done depends on the equivalence assumption for the surrogate models.

If there actually is a difference in performance between the surrogate models (coins), the "traditional" assumption that the surrogate models are equivalent does not hold. In that case, not only is the distribution not binomial (as I said above, I have no idea what distribution to use: it should be the sum of binomials for each surrogate model / each coin). Note however, that this means that the pooling of the results of the surrogate models is not allowed. So neither is a binomial for $n$ tests a good approximation (I try to improve the approximation by saying we have an additional source of variation: the instability) nor can the average performance be used as point estimate without further justification.

If on the other hand the (true) performance of the surrogate is the same, that is when I mean with "the models are equivalent" (one symptom is that the predictions are stable). I think in this case the results of all surrogate models can be pooled, and a binomial distribution for all $n$ tests should be OK to use: I think in that case we are justified to approximate the true $p$s of the surrogate models to be equal, and thus describe the test as equivalent to the throwing of one coin $n$ times.

cbeleites unhappy with SX
  • 34,156
  • 3
  • 67
  • 133
  • Hi @cbeleites, I just commented that my CV analysis results in 2 unique values for that particular dataset (some other datasets have N unique values, with N usually less than 5), just as amoeba described above. Given this, how can I show that my predictions are stable using just my single dataset and CV? Regarding a binomial distribution, I was considering the Agresti-Coull interval (can work for high success rate / 100% success rate without glitching out). It seems you're saying I can use a binomial distribution, but I'm still unclear how I can justify that assumption of same prob of success. – Sean Feb 28 '14 at 23:11
  • @cbeleites: [I deleted my previous comment to your answer and copy here one part of it.] But what does it mean to show that "the predictions are stable"? Repeated CVs will not give absolutely identical results. For example, let's say OP runs 1000 repetitions of CV and gets error rates from 0/120 to 2/120 with a certain distribution. Is there any way to combine this variance with the binomial variance? And for which $p$ does one compute binomial interval then? – amoeba Feb 28 '14 at 23:25
  • @Sean: in MATLAB you can very easily compute exact binomial confidence intervals using `bionofit` (it uses [Clopper-Pearson](http://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval#Clopper-Pearson_interval) method). I tried it now: `binofit(0,120)` gives [0, 0.030] interval, and `binofit(1,120)` gives [0, 0.046]. I see that *both* are larger than the CI that my method gives you ([0, 0.008]), so it looks like I was wrong all along and in your case binomial variance is dominating and cannot be disregarded. Still, how to combine all that in one interval, I do not know. – amoeba Feb 28 '14 at 23:31
  • @amoeba: I wrote up something simple to calculate the Agresti-Coull interval: (0,120) gives [0,0.037] and (1,120) gives [0,0.050], results that are quite close to your Clopper-Pearson calcs. But again, this brings us back to one of the original question: can I justify using a binomial distribution, and if so, how? This confidence interval / reliability testing issue is quite a nontrivial, but interesting problem -- great discussions on this thread over the past 24 hours! Hoping to hear more from you guys, thanks for all the input and comments. – Sean Feb 28 '14 at 23:46
  • 1
    @amoeba: I have no idea how to combine the binomial distribution with the unknown distribution due to instability into one confidence interval. So I report the observed percentiles for the (in)stability and binomial c.i. for the finite test sample size. How to combine them is one of the research questions I keep back in my head, but so far I've neither found a solution nor met anyone who has. I guess we arrived at the forefront of research... – cbeleites unhappy with SX Mar 01 '14 at 14:44
  • @cbeleites: Thanks for providing a link to your journal article (just read it) and the detailed information in your post. I think your approach should be fitting for what I'm trying to do. I have two quick clarifications regarding your post: (1) For reporting the variance of instability over the iterations, I assume you mean there are 'k' folds per iteration (e.g. 10), 'i' iterations (e.g. 1000), and n data points in each sample (e.g. 120)? (2) The binomial CI for the 'averaged observed performance' refers to the average of all the probabilities derived from 'i' iterations of the CV? ... – Sean Mar 01 '14 at 23:08
  • … and in the CI around this average probability (if I’m using the Agresti-Coull interval), the ‘n’ trials refers to the number of trials PER ‘i’ iteration of the CV (e.g. 120) in my case? This interval calculation should be one of many that would work for my situation. The average probability in my case is a non-integer, so I’ll look into the Bayesian approach – otherwise I’ll take the more conservative approach and use worst observed performance (119 successes of 120 trials). – Sean Mar 01 '14 at 23:09
  • (1) yes. (2) yes, the grand mean of sucesses over all $i$ iterations $\cdot k$ folds $\cdot \frac{n}{k}$ left out cases for each fold/surrogate model (in my drawing the $\frac{23}{27} = 85\,\%$). $n$ for the binomial distribution is the number of independent cases you have, so yes: 120 in your case for accuracy (in my drawing: 9), 80 and 40 respectively for sensitivity and specificity (in my drawing: 5 and 4 / 4 and 5 for the other class) etc. – cbeleites unhappy with SX Mar 02 '14 at 00:22
  • @cbeleites: how do you deal with the correlation between the errors between different CV-folds? this correlation inflates the variance of the mean accuracy (over all folds) so it's not binomial any more, rendering the CI too optimistic. – Trisoloriansunscreen Mar 02 '14 at 17:08
  • @Tal: You mean within each iteration? I'd expect the surrogate models within each iteration to be slightly *less* similar than the ones I use for measuring instability. Or do you mean that all surrogate models during $i \times k$-fold c.v. are more similar to each other than surrogate models on proper new training data of that size would be? For the latter I have no idea how to esimate it (but IIRC the Bengio paper says something about it - I need to reread that one). But if the task is not to estimate generalization error of *a* model for this problem built with training size $n$ but for ... – cbeleites unhappy with SX Mar 02 '14 at 17:20
  • ... *the* model build with the data at hand, I think this is what we need. But anyways, I don't even know how to combine the instability variance (what distribution does/should/can we assume it to follow?) with the binomially distributed finite-test-set variance. Practially I think it is already a big advance if people start to realize that there is this instability variance and measure it to get an idea of its order of magnitude, and realize that iterations cannot overcome the fact that only a finite (and in my field far too small) number of idependent test cases is used. – cbeleites unhappy with SX Mar 02 '14 at 17:25
  • But I'd be *very* happy if you could make a suggestion how to deal with it! – cbeleites unhappy with SX Mar 02 '14 at 17:26
  • I have no reservations regarding the way you measure instability variance. However, my point is that if you use K-FOLD CV, the finite-test-set variance is not behaving according to a binomial distribution. I think that this what the Bengio reference is about. – Trisoloriansunscreen Mar 04 '14 at 19:58
  • If this is the case, then is there any way to give an appropriate error analysis for the results of a k-fold CV analysis? Do you guys have suggestions for any other statistical methods that would work for my scenario? I've done some ROC analysis, but haven't found anything else as of yet. – Sean Mar 05 '14 at 22:45
  • @Sean: Sorry, you read here about as much as I think I know about this topic. – cbeleites unhappy with SX Mar 06 '14 at 12:56
  • @cbeleites: Thanks for all your input. Do you have any thoughts regarding Tal's comment about the finite-test-set variance of the k-fold CV not behaving like a binomial distribution? Your prior explanation was that if repeated CV iterations are stable, then a binomial distribution can be utilized to construct proportion intervals (even if no true 'p' is known for the population -- still something I'm a little wary of). I just want to make sure I'm truly justified in assuming a binomial distribution. – Sean Mar 06 '14 at 18:00
  • @Sean: Let's start with the "easy" part of your questions: The fact that the true $p$ is unknown is no problem: this is usual for the parameter that is to be measured (works exactly the same way measuring a gaussian distributed parameter). As for whether you are allowed to use a binomial distribution, please see my updated answer. I think the practical conclusion is that you are able to show "experimentally" in certain situations that the binomial distribution is a justified approximation. I hope you are in this situation - if you are not it most likely means that your modeling is off anyways. – cbeleites unhappy with SX Mar 06 '14 at 20:45
  • @cbeleites: Thank you for the updated answer, that helps clarify your use of the binomial. For a quantitative justification for using this distribution (e.g. stability of predictions), should it be enough to report the instability variance (variance of the probabilities from all the iterations of the k-fold CV)? Which variance is most sensible to compare this with to show that the models are stable? – Sean Mar 06 '14 at 22:15
  • 1
    @Sean: Have you seen my [recent question](http://stats.stackexchange.com/questions/88809/significance-testing-of-cross-validated-classification-accuracy-shuffling-vs-b) about related issues? There is a very interesting (for me) discussion going on in the comments, and I am currently working on some simulations myself. I came to believe that binomial assumption is badly wrong! You might also be interested in several references provided there that claim the same thing. – amoeba Mar 07 '14 at 20:46
  • @amoeba: Thanks for the link to your thread, you did quite an interesting simulation there regarding the error behind the binomial assumption. Would you mind keeping me in the loop if you continue any discussions about this outside of CrossValidated? I have yet to find a concrete solution without any major caveats (as I've read in other publications such as those in your own thread). – Sean Mar 11 '14 at 17:55
  • 1
    @Sean: I will try to keep these two threads updated, which means that after (and if) the issue gets clarified further I will try to summarize the situation there and also to provide a new answer here. For now, have you noticed [this paper](http://linus.nci.nih.gov/techreport/conflimbiosubmission0107.pdf) linked in the other thread? The authors discuss exactly your question, and provide a bootstrap procedure that they claim works well. If I were to write a reply to your question right now, I would recommend their procedure. But it would make sense first to check 24 papers that cite that paper. – amoeba Mar 11 '14 at 18:05
  • @Sean: amoeba's advise is good. There is just one point you need to keep in mind here: your classes are not balanced. Thus, more than half (1/9 + 4/9 = 5/9 ≈ 55%) of the randomly labeled cases do have the correct label. Double-check that this doesn't mess up the permutation test. On a quick glance, the examples of the Jiang paper use equal sample sizes in each class. – cbeleites unhappy with SX Mar 11 '14 at 19:52
  • @Sean: if you like to follow the further discussion between amoeba and me more closely (and possibly to contribute), send me an email: claudia dot beleites at ipht minus jena dot de. (I'll delete this comment tomorrow). – cbeleites unhappy with SX Mar 11 '14 at 19:53
4

I think your idea of repeating cross-validation many times is right on the mark.

Repeat your CV let's say 1000 times, each time splitting your data into 10 parts (for 10-fold CV) in a different way (do not shuffle the labels). You will get 1000 estimations of the classification accuracy. Of course you will be reusing the same data, so these 1000 estimations are not going to be independent. But this is akin to bootstrap procedure: you can take standard deviation over these accuracies as the standard error of the mean of your overall accuracy estimator. Or a 95% percentile interval as the 95% confidence interval.

Alternatively, you can combine cross-validation loop and the bootstrap loop, and simply select random (maybe stratified random) 10% of your data as a test set, and do this 1000 times. The same reasoning as above applies here as well. However, this will result in higher variance over repetitions, so I think the above procedure is better.

If your misclassification rate is 0.00, your classifier makes zero errors and if this happens on each bootstrap iteration, you will get zero wide confidence interval. But this would simply mean that your classifier is pretty much perfect, so good for you.

amoeba
  • 93,463
  • 28
  • 275
  • 317
  • Hi @amoeba, thanks for your response. Would you mind explaining a bit more regarding your first suggestion in repeating the CV 1000 times by random permuting the samples? Should there be a pre-established proportion of test set : training set (e.g. 10:90 for the 10-fold cross-validation)? I guess I'm a little unclear how repeating the 10-fold validation would increase the variance over time. – Sean Feb 27 '14 at 21:29
  • Well, each 10-fold cross-validation splits data in 10 parts and on each fold you take 9 parts as training and 1 part as test, so you always have 10:90 proportion. The main idea here is that each sample is predicted exactly once, so 10 folds give you 10 *independent* estimations of accuracy. My suggestion is to repeat this whole procedure many (e.g. 1000) times, each time splitting data into 10 parts in a different (random) way. The resulting 1000 accuracies will not be independent, but their sampling distribution should provide the confidence interval. Your last sentence I did not understand. – amoeba Feb 27 '14 at 22:28
  • I must add that I am not a big expert on these things. I would be very grateful to @cbeleites, who is often commenting here about cross-validation, if she could confirm that my intuition is correct (in particular that doing repeated 10-fold CV is better than repeated prediction of random 10% of the data). – amoeba Feb 27 '14 at 22:32
  • Ah okay, I understand what you're saying -- just make sure the data isn't being split into the *same* 10 folds for every iteration. I had misread your first statement, hence that incorrect last sentence in my previous comment. Apologies for that. I'm also looking into seeing if a logistic regression model would be useful for my situation. Thanks very much for taking the time to comment and providing some helpful advice, I appreciate it. And @cbeleites, I'd appreciate any input from you as well! – Sean Feb 27 '14 at 23:54
  • I would use the label shuffling procedure suggested by @amoeba, but it's important to note that the distribution you'll get will describe the accuracy of the classifier given the null assumptions that the labels don't matter. This is great if you want to test whether your result is significantly above chance, but it conveys no information regarding the variability of your actual accuracy. In other words, it's not a confidence interval. – Trisoloriansunscreen Feb 28 '14 at 15:02
  • 1
    I'm afraid that the second procedure @amoeba suggested is too optimistic: a non-perfect classifier can have a perfect performance on a given dataset (for example, assume you have only 4 samples - it's a 1:8 to classify all of them correctly by chance). As amoeba noted, measuring the variance over different allocations of train-test folds will produce 0 width confidence interval, which is clearly incorrect in this case. – Trisoloriansunscreen Feb 28 '14 at 15:09
  • @Tal: I did *not* suggest to do a shuffling procedure, but I see now that my wording was unfortunate and I will improve it now. What I suggested, is repeated CV with different splits. This should give confidence intervals, as desired by OP. Your worry about tiny sample size I don't understand: random classifier will show chance level performance on repeated CV, even if there are only 4 samples. – amoeba Feb 28 '14 at 15:24
  • 1
    I think that ultimately, this problem comes down to finding the probability of observing data that is different than what I haven't already observed. Getting confidence intervals for my sample is what @amoeba suggested for my original question (I used random folds for each CV iteration), and the result looks more realistic (95% CI: [0.0028, 0.0033]). However, I don't know if there's another technique that would be better for future data prediction. Perhaps some sort of model-based approach where I fit curves to my data and calculate their overlap? – Sean Feb 28 '14 at 16:35
  • 3
    @amoeba: Thank you for the clarification, I guess I didn't read your answer carefully enough. Yet, I'm still troubled about an optimistic bias of this approach (both procedures). By measuring accuracy while trying different CV splits, you estimate the variability that is caused by the arbitrary splitting. Yet, you ignore the fact your entire data is a random sample of larger population of observations (that you didn't collect). If you have a small dataset that by chance achieves perfect performance (regardless of CV splits), your confidence interval is zero and this is incorrect. – Trisoloriansunscreen Feb 28 '14 at 16:44
  • @Tal: I see your point, but do you have a better procedure in mind? – amoeba Feb 28 '14 at 16:44
  • 1
    @amoeba: It's tricky, since you can't bootstrap the observations themselves (consider a nearest neighbor classifier in such case). I'm struggling with that problem myself, let's see if someone else comes up with an idea. – Trisoloriansunscreen Feb 28 '14 at 16:47
  • @amoeba: Tal is right. The particular setup of the cross validation hides the variance due to the finite test set (the binomial one). Looking only at the variation between cross validation runs measures stability, but not the total variance the error estimate is subject to. – cbeleites unhappy with SX Feb 28 '14 at 17:11
  • @Sean: I doubt you can get CI as you reported above with your sample size. Note that you should not take 95% confidence interval of the mean of your distribution of 1000 estimations! Instead, you should take 95% *percentile* interval, i.e. almost the whole range. Are you sure you did that? – amoeba Feb 28 '14 at 17:13
  • @amoeba: I calculated that earlier CI by taking the average (xbar) of my 1000 values, then calculating xbar ± 1.96*stdev / sqrt(1000) for the 95% interval... which sounds like what you said not to do! Of the 1000 calculated values, there are only 2 unique values (0 (300x) and 0.01 (700x)) -- do you mean a 95% percentile interval as the 95% range between these two values, e.g. [0.0025,0.00975]? – Sean Feb 28 '14 at 22:59
  • @Sean: my understanding is that you should take 2.5--97.5 **percentile** range of your values. In case you got 300 times zero errors and 700 times one error, this 95% percentile range is simply [0/120, 1/120] = [0, 0.008]. – amoeba Feb 28 '14 at 23:09
  • @Tal: I think you spotted the problem: there are (at least) 2 sources of variance here, test sample (size) and instability of the surrogate models. I'd appreciate your thoughts on my answer. – cbeleites unhappy with SX Mar 01 '14 at 17:35
3

Classification error is both discontinuous and an improper scoring rule. It has low precision, and optimizing it selects on the wrong features and gives them the wrong weights.

Frank Harrell
  • 74,029
  • 5
  • 148
  • 322
  • This can hardly be a problem for the OP if he gets 99-100% cross-validated classification accuracy. – amoeba Mar 01 '14 at 14:27
  • 1
    @amoeba: It can be a problem also if correct proportions close to 100 or 0 % are observed: in contrast to performance measures that rely on continuous scores, any kind of performance that is measured after dichotomizing (hardening) the continuous classification score cannot indicate the predictions are getting close to the decision border as long as they are still on the correct side. However, IMHO there are valid reasons to report the proportion-type performance measures (e.g. if your readers/collaborators understand them, but don't understand e.g. Brier scores). I didn't want to open that... – cbeleites unhappy with SX Mar 01 '14 at 15:33
  • ... line of discussion as there was no indication of optimization in the question (which is where this becomes really important). – cbeleites unhappy with SX Mar 01 '14 at 15:33
  • If you are computing proportion classified "correctly" you must be doing it for a reason, e.g., to make a judgement or take an action. The proportion is misleading for these purposes. – Frank Harrell Mar 01 '14 at 15:47
  • 1
    @FrankHarrell: Well, the reason I guess is to report it in a paper. Do you think people should stop reporting classification accuracies at all? – amoeba Mar 01 '14 at 15:55
  • Yes. Probability accuracy scoring rules are much more informative, have higher precision, and can be optimized by the correct model. They are also not arbitrary, i.e., don't require any arbitrary cutoffs. – Frank Harrell Mar 02 '14 at 03:11
  • @FrankHarrell Where can I read a longer treatment of this issue? E.g what loss function $L(\hat p_i, y_i)$ we want to use if not 1[round($\hat p_i) = y_i$]? – Hatshepsut Apr 17 '16 at 02:01
  • Consider the Brier score and pseudo $R^2$ measures. These are proper accuracy scoring rules. You can supplement this with the $c$-index (concordance index = AUROC). – Frank Harrell Apr 17 '16 at 12:21