Is a lower training accuracy possible in overfitting (one class SVM)

Question

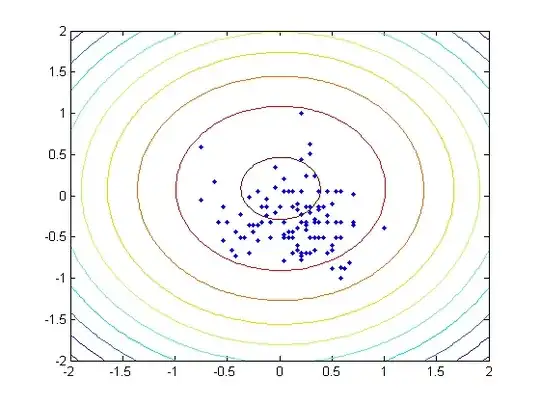
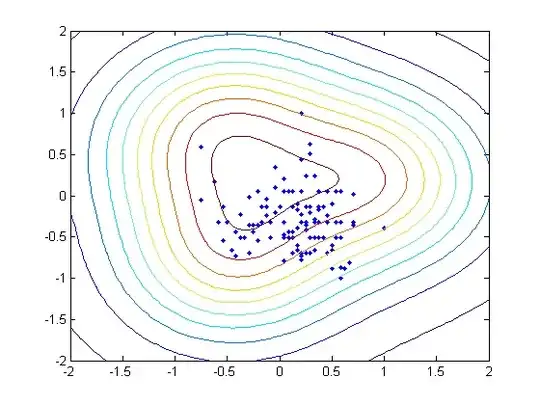
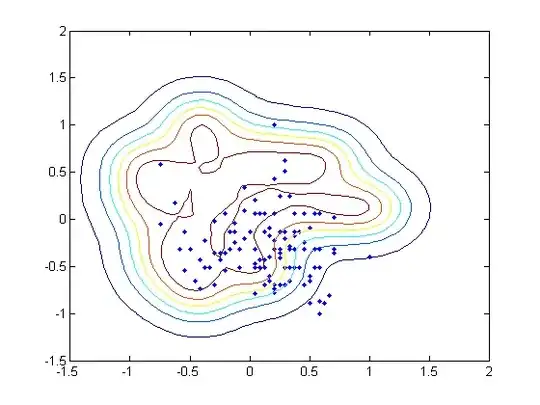
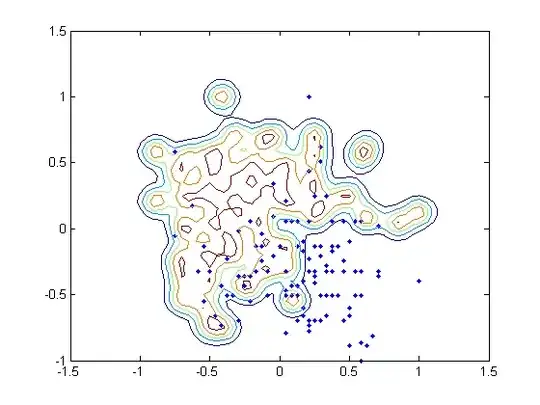
I am using the heart_scale data from LibSVM. The original data includes 13 features, but I only used 2 of them in order to plot the distributions in a figure. Instead of training the binary classifier, I treated the problem as a one-class SVM by only selecting the data labelled +1.

The $\nu$ is fixed to $0.01$ in my case, and I tried 6 different $\gamma$ values for my RBF kernel: $10^{-3}$, $10^{-2}$, $10^{-1}$, $10^{0}$, $10^{1}$, and $10^{2}$. Theoretically small $\gamma$ may lead to high bias and low variance, while large $\gamma$ may get the reverse, and tend to overfitting. However, my result indicates the statement above is only partially true.

1. As $\gamma$ increases, the number of support vectors are 3, 3, 3, 7, 35, and 89.

2. On the other hand, however, the training accuracy (the corrected classified data among 120) is 117, 118, 119, 117, 96, and 69. The training error increases dramatically.

3. I also tried to deal with the binary classifier, and the relation between $C$, $\gamma$ and the variance/bias performance is consistent with the 'theory' trend.

I was trying to understand why this 'contradiction' occurs with one class SVM.

I attached the contour of the 6 different hyperplanes below as well.

Answer 1

Proportion classified correctly is a discontinuous improper scoring rule that is optimized by a bogus model. I would not believe anything that you learn from it.

Answer 2

UPDATE

There is probably an numerical error with one class nu-svm in LibSVM. At optimum, some training instances should satisfy w'*x - rho = 0. However, numerically they may be slightly smaller than zero Then they are wrongly counted as training errors. Since nu is an upper bound on the ratio of training points on the wrong side of the hyperplane, numerical issues occur in calculating the first case because some training points satisfying y*(w'*x + b) - rho = 0 become negative.

This issue does not occur for nu-SVC for two-class classification.

The authors added this issue to their FAQ.

-----------OLD ANSWER BELOW-------------------------------------------------------------------------

Thanks for @cbeleites's note. I investigated the influence of both $\gamma$ and $\nu$ in one class SVM. I used 5-fold cross validation (but not the '-v 5' option in libsvm) bu shuffling the data 100 times and then average the accuracy (still use the proportion classified correctly). The result images show the training accuracy, testing accuracy, and generalization error (the difference between the former two) with different combinations of $\gamma$ and $\nu$.

Cbeleites is correct that $\gamma$ itself is not sufficient to determine the variance of the model. The underfitting is very clearly shown in subfigure(3), but it seems like there is only a slightly overfitting around the middle part ($\nu \approx 0.1$, $\gamma \approx 5$, I didn't locate in the exact coordinate). And there is the "longish optimum" as Cbeleites mentioned in the comment. Basically large $\gamma$ and $\nu$ might cause the underfitting but the overfitting dependence on the coefficient is not that evident. I used the logarithm of $\gamma$ and $\nu$ to show the smaller value region more clearly below.

Answer 3

Based on Dr. Harrell's suggestion, I tried Logarithmic and Brier scoring rule. Since libsvm does not support probability estimation on nu-svm, I had to do it with binary class SVM.

Some notes on the result image:

1. The proportion classified correctly is different with the '-b 1' option in training and testing. Since the other scoring rules are calculated with the '-b 1', it makes more sense to compare the last three sub-figures;

2. The maximal and minimal of the logarithmic and brier are the same ($\gamma$ $\approx 50$), at which the accuracy in sub-figure 2 is $0$, and in sub-figure 2 is $100 \% $. The functions are continuous but not monotone, so my concern in OP still exists.

The figures with only 2 features as it was in the OP: