5

I always think about the error term in a linear regression model as a random variable, with some distribution and a variance. So if the error terms come from this random variable, why do we say that they have a constant variance?

kanbhold
  • 755
  • 2
  • 9
  • 18
  • 3
    You might need to expand this a bit to explain what the apparent contradiction is supposed to be. – Scortchi - Reinstate Monica Feb 16 '14 at 18:25
  • It is one random variable isn't it? If the error terms come from this one random variable of course they will have the same variance. – kanbhold Feb 16 '14 at 18:31
  • 4
    "Error terms" is in the plural: they are a realization of one *multivariate* random variable, if you like. If you don't like that point of view, then you must view them as being realizations of multiple separate random variables (which might or might not have any properties in common). – whuber Feb 16 '14 at 18:36
  • If you're asking whether it's redundant to say of a model *both* that the error terms are realizations of e.g. a Gaussian random variable with mean zero & variance $\sigma^2$, *and* that they have constant variance, then yes it is. Constant variance is emphasized because in some models the variance is a function of the mean, or of a predictor, & therefore not constant. – Scortchi - Reinstate Monica Feb 16 '14 at 18:41
  • It may help you to read my answer here: [What does having constant variance in a linear regression model mean?](http://stats.stackexchange.com/questions/52089//52107#52107), which addresses this issue. – gung - Reinstate Monica Feb 17 '14 at 14:56

1 Answers1

3

The error term ($\epsilon_i$) is indeed a random variable. The normality assumption holds if it has Normal distribution - $\epsilon_i$ ~ $N(\mu,\sigma)$. You are right when you say:

I always think about the error term in a linear regression model as a random variable, with some distribution and a variance

The assumption of constant variance (aka homoscedasticity) holds if the dispersion of the residuals is homogeneous along the range of values in $X$ or $Y$. This pattern of dispersion can vary.

So if the error terms come from this random variable, why do we say that they have a constant variance?

One error observation alone does not have variance. The variances come from subsets of groups of error observations. For a better comprehension, look into this picture, borrowed from @caracal's answer here.

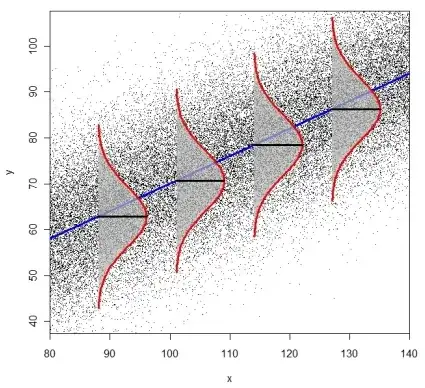
enter image description here

It also helps looking to some plots which illustrates the opposite of homoscedasticity (non constant variance).

Community
  • 1
Andre Silva
  • 3,070
  • 5
  • 28
  • 55
  • This answer appears to miss the point: how can the $\epsilon_i$ be considered "a" random variable when they are heteroscedastic? – whuber Feb 16 '14 at 22:16
  • 2
    "One error observation alone does not have variance." True, but it can be thought of as having been drawn from a distribution that does have a variance. – gung - Reinstate Monica Feb 17 '14 at 14:59