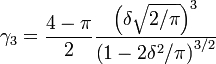Indeed, the "skew-normal family" has exploded in membership (the wikipedia article does not attest to this). So, let's consider the mother of them all, that has probability density function
$$f_X(x) = \frac{2}{\omega}\phi\left(\frac{x-\xi}{\omega}\right)\Phi\left(\alpha \left(\frac{x-\xi}{\omega}\right)\right)$$
where $\phi()$ is the standard normal pdf and $\Phi()$ the standard normal cdf. $\xi$ is the location parameter, $\omega$ is the scale parameter, and $\alpha$ is the skew parameter.
Closed-form solutions for the ML estimator do not exist. Method-of-Moments estimator provides closed forms as follows, assuming that all three parameters are non-zero (obviously if $\omega$ and/or $\xi$ are zero, then the steps below are simplified):
1) Obtain a MoM estimate $\hat \delta$ by solving for $\delta$ the expression for the skewness of the distribution,
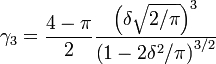
using the estimated sample skewness coefficient $\hat \gamma_3$.
2) Obtain an estimate $\hat \alpha$ using
$$\delta = \frac {\alpha}{\sqrt {(1+\alpha^2)}} \implies \hat \alpha = \frac {\hat \delta}{\sqrt{1-\hat \delta^2}}$$
3) Obtain a MoM estimate $\hat \omega$ by solving for $\omega$ the expression for the variance,
$$\hat \sigma^2_x = \omega^2\cdot \left(1-\frac{2\hat \delta^2}{\pi}\right)$$
using the sample variance and the estimated $\delta$ derived in the previous step
3) Obtain a MoM estimate $\hat \xi$ by solving for $\xi$ the expression for the mean of the distribution,
$$\hat \mu_x = \xi + \hat \omega \hat \delta\sqrt {2/\pi}$$
using the sample mean and the previous estimates.
And don't forget to propagate estimation error in this sequential procedure, as regards the estimator variance.