Why not use Beta(1,1) as boundary avoiding prior on a transformed correlation parameter?

Question

In Bayesian Data Analysis, chapter 13, page 317, second full paragraph, in the modal and distributional approximations, Gelman et al. write:

If the plan is to summarize inference by the posterior mode of $\rho$ [the correlation parameter in a bivariate normal distribution], we would replace the U(-1,1) prior distribution with $p(\rho) \propto (1 - \rho)(1 + \rho)$, which is equivalent to a Beta(2,2) on the transformed parameter $\frac{\rho + 1}{2}$. The prior and resulting densities are zero at the boundaries and thus the posterior mode will never be -1 or 1. However,...the prior density for $\rho$ is linear near the boundaries and thus will not contradict any likelihood.

Below is a plot of the PDF for the Beta(2,2) distribution.

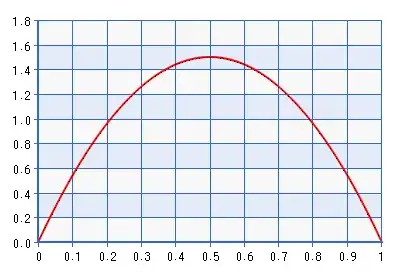
Although the plot is given for the domain [0,1], the shape is the same for the domain [-1,1] obtained by performing the inverse of the transformation described in the quote above. This is a fairly informative distribution! It gives about seven times the density to $\frac{\rho + 1}{2} = 0.5$ than it does to $\frac{\rho + 1}{2} = 0.3,0.97$. So in fact it would contradict the likelihood if the likelihood pointed toward something far from the boundaries, but even further from $\rho = 0$. Wouldn't a better boundary avoiding prior be Beta(1 + $\delta$,1 + $\delta$), where $\delta \rightarrow 0$. Take, for example, Beta(1.0001, 1.0001), plotted below:

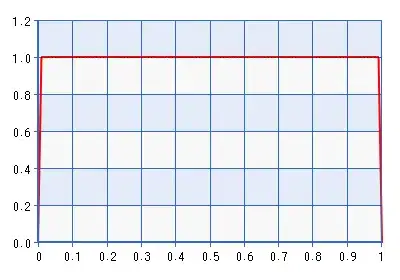
The trouble with this prior, of course, is that the density drops very sharply near zero, which may contradict the likelihood of it points to a space that is very very near a boundary. Which brings me to my question:

Why not just set the prior of the transformed correlation parameter to Beta(1,1)? Because the beta distribution density is zero for $\frac{\rho + 1}{2} = 0,1$, this is equivalent to the uniform distribution over the open interval (-1,1) rather than the closed interval [-1,1], and so is it not a boundary avoiding prior, and is it not preferable to a prior that places fairly strong belief in the probability that $\rho = 0$, which is only desirable if you actually have that belief?

More generally, isn't using the beta distribution by definition a boundary avoiding prior because its support is $0 < \frac{\rho + 1}{2} < 1$?

Answer 1

In cases where the likelihood function is maximized at $\rho=-1$, using Beta(1,1) over an open interval doesn't help since then there is no well-defined posterior mode. There is no point in the open interval that you could say is the posterior mode.

The book wants the prior to be linear at the boundaries, which uniquely selects Beta(2,2) out of all Beta distributions. But the book never precisely explains why linearity is so important.