I have a ratio of two random, (dependent or independent) normally distributed variables.
Knowing that the resulting Cauchy-distribution does not produce any moments. May I ask: Is there an approximation to a Cauchy distribution? Can I still get something out of my set of ratios?
The ratio of two arbitrary normal random variables is not in general Cauchy.
Even the ratio of two jointly normal random variables is not in general Cauchy.
Let's assume you're dealing with a ratio that does have a Cauchy distribution. Then all manner of quantities converge - including quantiles and many functions of quantiles, trimmed and winsorized moments, and cdfs.
Your question assumes that the distribution of the denominator is centered at 0. If this is so, the median and the mad will converge (to 0 and 1, respectively).
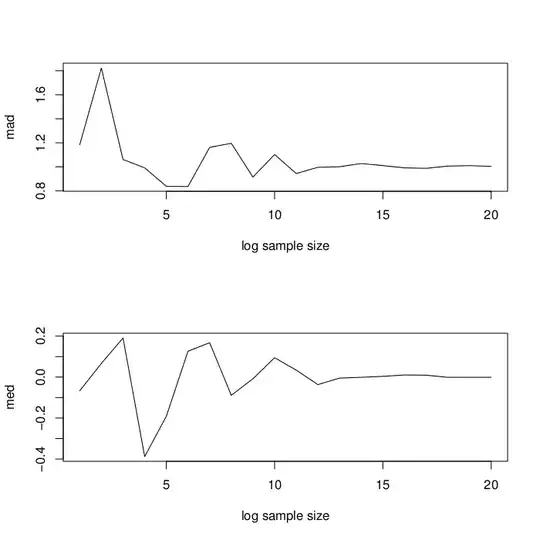
nn<-exp(seq(log(10),log(100000),l=20))
aa<-rep(NA,length(nn))
bb<-rep(NA,length(nn))
for(i in 1:length(nn)){
x1<-rt(nn[i],df=1)
aa[i]<-median(x1)
bb[i]<-mad(x1,constant=1)
}
par(mfrow=c(2,1))
plot(bb,type="l",ylab="mad",xlab="log sample size")
plot(aa,type="l",ylab="med",xlab="log sample size")
btw, you have to change the consistency factor in the computation of the mad from $1.4826=1/\Phi^{-1}(0.75)$ to $1=1/t^{-1}_{0.75}$ (the quantile function of the Cauchy distribution evaluated at $q=0.75$)
First, the ratio is Cauchy only if the denominator distribution is centered at 0. In any cases, the statistics on the ratio of $y$ and $x$ can be approximated as:
$$\hat{\mu}_{y:x} = \mu_y/\mu_x + \sigma^2_x * \mu_y / \mu_x^3 + cov(x,y) * \sigma^2_x * \sigma^2_y / \mu_x^2$$ $$\hat{\sigma}^2_{y:x} = \sigma^2_x\times\mu_y / \mu_x^4 + \sigma^2_y / \mu_x^2 - 2 * cov(x,y) * \sigma^2_x * \sigma^2_y / \mu_x^3$$
if one supposes that the variances are neglictable with respect to the mean (see the post How to parameterize the ratio of two normally distributed variables, or the inverse of one?).
However, I think that as suggested in other answers, using the quantiles would be more appropriated.
