147

I got this question during an interview with Amazon:

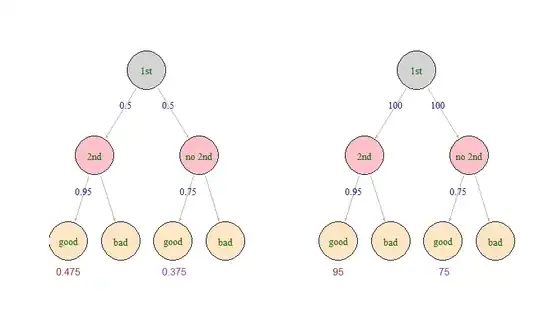
  • 50% of all people who receive a first interview receive a second interview
  • 95% of your friends that got a second interview felt they had a good first interview
  • 75% of your friends that DID NOT get a second interview felt they had a good first interview

If you feel that you had a good first interview, what is the probability you will receive a second interview?

Can someone please explain how to solve this? I'm having trouble breaking down the word problem into math (the interview is long over now). I understand there may not be an actual numerical solution, but an explanation of how you would walk through this problem would help.

edit: Well I did get a second interview. If anyone is curious I had gone with an explanation that was a combination of a bunch of the responses below: not enough info, friends not representative sample, etc and just talked through some probabilities. The question left me puzzled at the end though, thanks for all of the responses.

Tim
  • 108,699
  • 20
  • 212
  • 390
Rick
  • 1,431
  • 2
  • 11
  • 9
  • 5
    I'm not sure myself, but I'm thinking Bayes Rule may be the direction we should take this in? – nicefella Feb 10 '14 at 01:52
  • The answers below about Bayes' Rule are probably what the interviewer was looking for, but to be pedantic, to conclude anything you need to make some assumption about what "your friends " are as a subset of "All People". – Patrick Sanan Feb 10 '14 at 05:13
  • not to mention the relative sizes of the two groups of friends... – Asya Kamsky Feb 10 '14 at 06:42
  • 1
    The "% of your friends" makes this ambiguous. The question is probably designed to check how to proceed in uncertainty. – Andomar Feb 10 '14 at 12:59
  • 72
    The good news is that you have at least 24 friends, otherwise distinct subsets of them could not add up to 95% and 75%. – Andomar Feb 10 '14 at 12:56
  • 9
    Is this a statistician's sarcastically hilarious way of telling you you didn't get the job? – geotheory Feb 10 '14 at 14:47
  • @Dmitri: if it's 50% even though you feel you had a good interview, then that means that your feeling is completely irrelevant (apparently interviewees can't judge how well it went _at all_). That's unlikely, and the experience of your friends also shows there's a difference. – RemcoGerlich Feb 10 '14 at 14:58
  • @RemcoGerlich this is correct, the feeling is irrelevant. – Dmitri Feb 10 '14 at 15:09
  • Dmitri: don't you think that's extremely unlikely, that people can't judge how well they did _at all_? What do you base that on? – RemcoGerlich Feb 10 '14 at 15:28
  • 26
    The existence of multiple contradictory answers--a few of which are given below--convincingly demonstrates that the point of this question is not to obtain a mathematical answer but rather to see whether the interviewee thinks carefully about what assumptions need to be made in order to obtain a reasonable, defensible answer. Thus, we ought to consider any *single, definite* answer to this question to be incorrect--or at least not worthy of getting a job offer from Amazon. The answers that point out the ambiguities and discuss the assumptions are the ones that have merit. – whuber Feb 10 '14 at 16:01
  • 6
    @whubere this philosophy certainly explains AWS pricing - very hard to understand, no single answer there. – Dmitri Feb 10 '14 at 16:10
  • @RemcoGerlich Some people are optimists, some pessimists. For example I did not expect to get a job after my interview but I got it. So my expectations did not mean anything. – Dmitri Feb 10 '14 at 16:13
  • 1
    I am disappointed that my answer was converted to a comment. It deprived me of the possibility of earning reputation points. It must be some kind of initiation for the new users, but I've been SO member for a long time – Dmitri Feb 10 '14 at 16:15
  • @Andomar If your friends are representative then you must have had at least 40 friends who took the interview :) – JamesRyan Feb 10 '14 at 16:20
  • @Andomar & JamesRyan: I am curious, how did you arrive at 24 and 40 friends? – KM. Feb 10 '14 at 16:23
  • @KM: 19/20 for 95%, 3/4 for 75%, so 24 total. Can't divide further. – Andomar Feb 10 '14 at 16:35
  • 1
    @Dmitri I agree with you: your answer was an answer and should not have been converted to a comment. I am sorry this happened and I have undeleted the answer (and, accordingly, deleted the comment :-)). – whuber Feb 10 '14 at 17:05
  • 2
    @Dmitri: of course many people will get it wrong, still I feel it's very strange to say that the judgement of the interviewees is completely useless. If people's average judgement is only 0.1% better than a coin toss, then the answer isn't 50%. – RemcoGerlich Feb 10 '14 at 17:28
  • 1
    The only possible "correct" answer is 100%. - Namely the probability of *you* getting a second interview is unrelated to that of your friends in any meaningful way. Any other answer would indicate that you don't feel you have impressed the interviewers well enough and therefore shouldn't get a second interview. The numbers etc are just there to trip people up. – NotMe Feb 10 '14 at 17:36
  • 1
    The only possible "correct" answer is 50%. You do not belong to the set of **'your friends'** so rules 2 & 3 are irrelevant. You would default to the rule **'50% of All People who receive first interview receive a second interview'**. – MrWonderful Feb 10 '14 at 19:17
  • 1
    @MrWonderful True, you don't belong to the set of 'your friends'. However, 'your friends' is a sample of 'your social circle' that includes the entire population of that set with the sole exception of yourself. So it's highly probable that the data given on 'your friends' is substantially **more** representative of your own chances than the data given on the general population (especially if you believe that your friends are fairly similar to you in terms of whatever traits Amazon might be looking for in their candidates). – Kyle Strand Feb 10 '14 at 19:29
  • 2
    @MrWonderful The 50% answer is wrong, because it's about people in general, whereas the question is only about people who felt good about the interview. Different groups. – Brilliand Feb 10 '14 at 19:41
  • 1
    None of the answers posted so far go into the specifics of what assumptions could be made in order to solve this problem and what extra data would be needed to solve it given a particular assumption. Also, lots of the answers seem to imply that statistics about the general population are a better indication of your personal chances than statistics about your friend group, which is almost certainly not true. Unfortunately, I can't post my own answer since I'm a noob here and the question is locked. – Kyle Strand Feb 10 '14 at 19:41
  • @MrWonderful, I might be swung in your direction. I agree 2&3 don't apply. Which leaves 50% of the universal population goes one way or another. However, the difference here *might* be that 50% of the people didn't understand the question. – NotMe Feb 11 '14 at 03:24
  • Just out of curiosity, does Amazon actually employ statisticians? – RobertF Feb 11 '14 at 16:05
  • 1
    @RobertF They must employ loads of statisticians - how else would they set up the calculations behind things like their recommendations system? Large amounts of their revenue depends on predictive models accurately estimating the probability of a given customer liking a given item. Then there's site analytics, warehouse efficiency analytics, pricing... (p.s. surely the correct answer is "What's the sample size, and am I a representative example of the sample?") – user56reinstatemonica8 Feb 11 '14 at 16:55
  • Case 1: I have 20 friends that got 2nd interviews. 1 didn't think the 1st went well. I also have 4 friends that didn't get a 2nd interview and 3 of them thought they did well in the 1st. Case 2: I have 20M friends that got 2nd interviews. 1M didn't think the 1st interview went well. I still have 4 friends that didn't get a 2nd interview and 3 of them thought they did well in the 1st. I don't believe the rules, AS STATED, can be used to make any better assessment than the first rule alone unless you assume 1st rule applies exactly to your group of friends. That's why I'd stick with 50%. – MrWonderful Feb 11 '14 at 17:18
  • I do hope the person who made this question, as well as the one who asks, realises the ambiguity and will not blindly follow the answer sheet like a poor teacher. – gerrit Feb 11 '14 at 19:41
  • No need to overcomplicate things. 'your friends' falls under the 'all people' category and it says "50% of all people who receive a first interview receive a second interview" regardless of how they felt. So regardless of how your friends (or you) feel, 50% receive a second interview, so the answer is 50%. Don't let your feelings get in the way. – user2719875 Feb 11 '14 at 20:48
  • @Andomar can u pls elaborate a little on how you got 24 as atleast friends figure? – om252345 Feb 12 '14 at 13:56
  • 1
    @user2719875 If I say: "50% of all interviewees get a second interview. 90% of people with a masters get a second interview. 10% of people without a masters get a second interview. You have a masters" What do you think your chances of getting a second interview is? If you say 50% I'm going to rip my eyes out. – Cruncher Feb 12 '14 at 14:34
  • 1
    @KM and Andomar, 95% and 75% of your friends should be an integer value. 40 is the lowest number that works. – Ari Feb 12 '14 at 22:35
  • @MrWonderful The idea is that your set of friends, are all in the set of all people. If your set of friends is big enough, then this subset is representative of the larger set. The only thing in question is how many of your friends interviewed. – Cruncher Feb 14 '14 at 20:02
  • Maybe this question is why Amazon is not yet market leader in anything - though appears to be in many things . Ambiguity does solve real life problems . This question has ambiguity though looks genuine . – Nishant Feb 25 '14 at 20:24
  • @Ari It's not "95% of your friends" and "75% of your friends", it's "95% of (your friends that got a 2nd interview)" and "75% of (your friends that did not get a second interview)". So the two denominators are different. The minimum denominators are 20 and 4 respectively, so 24 is the correct minimum number of friends. – Tim Goodman May 15 '14 at 00:07
  • This is a standard question to test the understanding of Bayesian theorem..... – Tony Mar 28 '19 at 09:00

15 Answers15

161

Say 200 people took the interview, so that 100 received a 2nd interview and 100 did not. Out of the first lot, 95 felt they had a great first interview. Out of the 2nd lot, 75 felt they had a great first interview. So in total 95 + 75 people felt they had a great first interview. Of those 95 + 75 = 170 people, only 95 actually got a 2nd interview. Thus the probability is: $$\frac{95}{(95 + 75)}=\frac{95}{170}=\frac{19}{34}$$

Note that, as many commenters graciously point out, this computation is only justifiable if you assume that your friends form an unbiased and well distributed sampling set, which may be a strong assumption.

Vincent Gelinas
  • 1,262
  • 1
  • 9
  • 5
  • 3
    Agrees with my answer. Nice thought process. – ahwillia Feb 10 '14 at 02:27
  • 23
    (+1) This is a good use of Gigerenzer's "natural frequencies" approach to Bayes rule computations. – dimitriy Feb 10 '14 at 02:39
  • 27
    Even though we live in a facebook age, where all people, even unknown, may be considered friends, the question was quite specific - 50% of ALL PEOPLE got 2nd interview and 75% of YOUR (optimistic) FRIENDS did not get the 2nd interview. Thus I think your answer is missing the most important part. Amazon wanted to see how friendly you are :) – Krystian Feb 10 '14 at 08:38
  • 4
    I just signed up only to +1 this answer. :). Awesome explanation bro. – Mithun Satheesh Feb 10 '14 at 12:49
  • 11
    I think it would be nice to mention that you can make this guess (answer is 95/(95+75)) only if you believe that your friends is an unbiased and well distributed sampling set (because they are not all the people). Like it is done with surveys - if you want to make a good guess you need to pick a good sampling set. – Ski Feb 10 '14 at 14:15
  • 1
    But those #s are only based on his friends, which is not a set he falls into. So, why would they apply to him? – MDMoore313 Feb 10 '14 at 15:48
  • This is also the method described in pop math book "the Joy of X" – WetlabStudent Feb 10 '14 at 16:30
  • Wrong. Why would *your* chances of getting a second interview be 19/34? Are you saying that you feel you are in the middle pack between you and your "friends"? What if you have 543 friends that interviewed? How does their results impact you at all? – NotMe Feb 10 '14 at 17:39
  • @ChrisLively The question is about people who thought they had a good interview. The 50% number is about people in general. It can't be applied directly. – Brilliand Feb 10 '14 at 19:33
  • There is no guarantee that 50% of **your friends** received a second interview. We only know that (1) a multiple of 20 friends **did** get a second interview, and (2) a multiple of 4 friends **did not** get a second interview (assuming the "75%" and "95%" figures are exact figures). This completely invalidates your answer, since there's really no way to correlate the information given on the general population with the information given about your friends, and you can make additional assumptions to allow you to arbitrarily determine the probability of getting a second interview. – Kyle Strand Feb 10 '14 at 19:33
  • 1
    Doesn't this solution presume that all persons that participated in these interviews are all your friends? Or is this "friends discrepancy" just an artifact of the OP's recollection of the problem? – broc.seib Feb 10 '14 at 20:16
  • I made a diagram for this method: http://imgur.com/ApfvzkV Here, the solution is `(sum of vertical stripe areas)/(sum of vertical AND horizontal stripe areas)`. The sizes are "sort of" to scale. I deliberately made the orange quad uneven (to underscore that your friends may not be an even subset) and not a subset of interviewees (because surely you have friends other than fellow interviewees!). Note that in this case, we're not told if our friends are a random sample - so I think it's fair to assume that they are (even though they probably aren't). It could be reworded to say "random survey". – Superbest Feb 10 '14 at 23:01
  • 1
    I'm surprised no one has tried to apply statistical methods for accounting for error in a small sample size. – Brilliand Feb 10 '14 at 23:05
  • This answer assumes that only people who felt they did well on the first interview scored a second interview. I don't see a basis for that assumption. – Derek Gusoff Feb 11 '14 at 01:51
  • 1
    @Brilliand: The question is about the Interviewee specifically. It makes statements which are unrelated, and ultimately a diversion anyway. The purpose is to see if the Interviewee can cut through the garbage. If your answer is anything less than 100%, I'm pretty sure the likelihood of you getting a call back just dropped at least slightly. – NotMe Feb 11 '14 at 03:20
  • @ChrisLively It's not garbage. By the same metric, you can't say the odds are not 50% either. You are NOT the other people that interviewed. Whether they got an interview or not is completely irrelevant to whether or not YOU get an interview. They're giving you a set of people, such that a higher % of them in one group, got an interview. Then saying whether or not you're in that group is irrelevant is to completely disregard what stats is ALL about. Looking at information given, and using it to arrive at some probability.. – Cruncher Feb 11 '14 at 15:09
  • 3
    @ChrisLively If I gave you 2 candidates. I said "Candidate 1 felt really good about his interview, candidate 2 did not." Then I tell you that one of them will get a second interview and one will not. Who will you bet on? If you're willing to bet on the guy that thinks he blew it, then I will take that bet all day long sir. – Cruncher Feb 11 '14 at 15:13
  • And if the population of the 75% is only 4 people, the chances of them representing the population as a whole is slim to none! You're equally weighting groups of unknown and possibly widely varying sample sizes (this should sound unbelievably vile to you). This is akin to averaging averages. Your analysis seems highly, highly suspect to me. – ErikE Feb 12 '14 at 18:46
  • As others mentioned, you need to justify the set of your friends is a reasonable sample. Since 95% and 75% of your friends should be an integer value. 40 is the lowest number that works. – Ari Feb 12 '14 at 22:43
  • As others mentioned, you need to justify the set of your friends is a reasonable sample. 95% and 75% of your friends should be an integer value. 40 is the lowest number that satisfies this, which is greater than the common 30 rule of thumb (http://stats.stackexchange.com/questions/2541/is-there-a-reference-that-suggest-using-30-as-a-large-enough-sample-size) – Ari Feb 12 '14 at 22:43
  • @ari It's only 24, comprised of 19/20 (95%) and 3/4 (75%). – ErikE Feb 13 '14 at 21:58
  • @Cruncher. That's not even close to the amazon question. Let's modify that to: 2 candidates. Candidate 1 felt really good; Candidate 2 did not. 1 will get a second interview; what are *your* chances of getting a second interview?" The answer is based on whether or not you feel that you will get a second interview. As I said, all the details are garbage. They are, in a humorous way asking how you think you are doing. If you fall back to some mental gymnastics to try and justify a percentage then you've failed. – NotMe Feb 14 '14 at 15:34
  • @ChrisLively First of all, I wasn't restating the question. I was giving an example operating under the constraints in the question. You also didn't answer it. If you would rather bet on the one that felt good about the interview, then you have conceded that feeling good about the interview has SOME bearing on you getting a second interview. That is it. In your modification you do not use the given information at all. – Cruncher Feb 14 '14 at 15:37
  • @ChrisLively I concede that you are correct iff the question was changed from 'If you feel that you had a good first interview, what is the probability you will receive a second interview?' To 'what is the probability you will receive a second interview?'. But that is not what the question says. – Cruncher Feb 14 '14 at 15:39
105

Let

  • $\text{pass}=$ being invited to a second interview,
  • $\text{fail}=$ not being so invited,
  • $\text{good}=$ feel good about first interview, and
  • $\text{bad}=$ don't feel good about first interview.

$$ \begin{align} p(\text{pass}) &= 0.5 \\ p(\text{good}\mid\text{pass}) &= 0.95 \\ p(\text{good}\mid\text{fail}) &= 0.75 \\ p(\text{pass}\mid\text{good}) &= \;? \end{align} $$

Use Bayes' Rule

$$ p(\text{pass}\mid\text{good}) = \frac{p(\text{good}\mid\text{pass}) \times p(\text{pass})}{p(\text{good})} $$

To solve, we need to realize that:

$$ \begin{align} p(\text{good}) &= p(\text{good}\mid\text{pass})\times p(\text{pass}) + p(\text{good}\mid\text{fail})\times p(\text{fail}) \\&= 0.5(0.95 + 0.75) \\&= 0.85 \end{align} $$

Thus:

$$ p(\text{pass}\mid\text{good}) = \frac{0.95 \times 0.5}{0.85} \approx 0.559 $$

So feeling good about your interview only makes you slightly more likely to actually move on.

Edit: Based on a large number of comments and additional answers, I feel compelled to state some implicit assumptions. Namely, that your friend group is a representative sample of all interview candidates.

If your friend group is not representative of all interview candidates, but is representative of your performance (i.e. you and your friends fit within the same subset of the population) then your information about your friends could still provide predictive power. Let's say you and your friends are a particularly intelligent bunch, and 75% of you move on to the next interview. Then we can modify the above approach as follows:

$$p(\text{pass}\mid\text{friend})=0.75$$ $$p(\text{good}\mid\text{pass, friend})=0.95$$ $$p(\text{good}\mid\text{fail, friend})=0.75$$ $$ p(\text{pass}\mid\text{good, friend}) = \frac{p(\text{good}\mid\text{pass, friend}) \times p(\text{pass}\mid\text{friend})}{p(\text{good}\mid\text{friend})} = \frac{0.95 \times 0.75}{0.85} \approx 0.838 $$

ahwillia
  • 2,406
  • 1
  • 14
  • 26
  • 10
    This is true only if we assume that *your friends* are representative of the overall group. – gerrit Feb 10 '14 at 09:59
  • I'm not sure why u defined 'bad' there ... but i found you solution as the only viable one throught all the answers – Decebal Feb 10 '14 at 12:42
  • What is the difference between $p(good|pass)$ and $p(pass|good)$ ? Is the combination not commutative? – Iain Samuel McLean Elder Feb 10 '14 at 15:00
  • "So feeling good about your interview only makes you slightly more likely to actually move on." Really? This could just be a symptom of the factors used to decide if you pass, not itself a factor. My feeling good about the interview does not change how well I performed. In fact, the entire analysis is based on the idea that how good you feel is itself a cause for passing/failing. – AJMansfield Feb 10 '14 at 16:35
  • @gerrit: Actually, it's only true if other things are also true, such as that you are in the middle of the pack with regards to comparing yourself to your friends. Which, if you have a lot of friends would imply that you think a lot of other people are better than you. – NotMe Feb 10 '14 at 17:41
  • @AJMansfield, relative probabilities do not imply causation. If P(A,B) != P(A)P(B), it means they are not independent. A might cause B, B might cause A, or A and B may have a common causative variable deeper down. – highBandWidth Feb 10 '14 at 18:45
  • 2
    While this answer and Vincent's answer come to the same result, I think this answer gives a more general explanation. This question is like a stock exercise in bayesian probability. – Ask About Monica Feb 10 '14 at 20:57
  • @IainElder $p(\text{pass} | \text{good})$ is the probability that you will pass given that you feel good about the interview. You could interpret it like this: if I knew that you feel good, how firmly would I believe that you will pass? $p(\text{good} | \text{pass})$ is the probability that you feel good about the interview given that you will pass (if I knew that you will pass, how firmly would I believe that you feel good?) Those are clearly different probabilities, and they are related to each other by the Bayes Theorem. – Rafael S. Calsaverini Feb 11 '14 at 13:15
36

The question contains insufficient information to answer the question:

$x$% of all people do A

$y$% of your friends do B

Unless we know the population size of all people and your friends, it is not possible to answer this question accurately, unless we make either of two assumptions:

Edit: Do also read the comment by Kyle Strand below. Another aspect we should consider is how similar am I to my friends?. This depends on whether one interprets you as the person spoken to or as an unspecified individual or group of individuals (both usages exist).

Community
  • 1
gerrit
  • 1,397
  • 11
  • 28
  • 2
    This is the only correct answer thus far. – akappa Feb 10 '14 at 17:24
  • 1
    I think I agree... – Behacad Feb 10 '14 at 18:16
  • 8
    There's an additional assumption you're making here: the question doesn't ask how likely *an arbitrary candidate* is to get a second interview: it asks how likely *you* are to get a second interview. By pondering whether your friend group is a representative sample of the general population, you're ignoring the possibility that you are more similar to your friends than you are to members of the general population, in which case data about your friends might be more indicative of your own chances than data about the general population is. – Kyle Strand Feb 10 '14 at 19:55
  • I would suppose that somewhere here the keystone is. The question is whether you are similar to your friends, or whether you are not. So maybe this is the best answer at the interview: "Depends on whether my friends are similar enough to me or not. I assume they are quite, so the answer is somewhere inbetween 50% and 59%". – yo' Feb 11 '14 at 14:27
  • 2
    Another key piece of missing information is *when* my friends were evaluated for their feelings about their interview. I am being asked *before* I know whether I have a second interview, but what if all my friends were evaluated after they knew whether they would receive a second interview? That knowledge could have changed their self-assessment, making their a posteriori feelings not directly comparable to my a priori assessment of my own performance. – Jonathan Van Matre Feb 11 '14 at 19:36
25

The answer is 50%. Particularly since it was an interview question I think Amazon wanted to test the candidate to see if they could spot the obvious and not be distracted by the unimportant.

When you hear hoofbeats, think horses, not zebras - reference

My explanation: The first statement is all the information you need.

50% of All People who receive first interview receive a second interview

The other two statements are just observations. Feeling you had a good interview does not increase your chances of having a second.

Although statistically the observations may be correct I believe they cannot be used to predict future outcomes.

Consider the following.

  • 2 shops sell lottery scratch cards
  • After selling 100 cards each a customer gets a winning card from shop 1
  • Statistically you could say that shop 1 now has a greater chance of a person getting a winning ticket, 1 in 100 compared to 0 in 100 for shop 2.

We understand this is not true. The reason it is not true is because in this example past events will not have a bearing on future outcomes.

CeejeeB
  • 423
  • 3
  • 4
  • 21
    Everything is just an observation. Reminds me about the anecdote, what is a probability of getting hit by the bus. 50%, you either get hit, or not. – mpiktas Feb 10 '14 at 08:58
  • 3
    That would be my response too. My reasoning being that the number of `my friends that had an interview at Amazon` is completely drowned out by the `all people hat had an interview at Amazon`. – deroby Feb 10 '14 at 09:24
  • 5
    deroby, I think you should ask if your friends is a reasonably well distributed measurement set. Even if they are completely drowned by all the other people they still can provide valuably correct insights. This is how surveys work. – Ski Feb 10 '14 at 13:58
  • *"Feeling you had a good interview does not increase your chances of having a second."* -- This is a reasonable assumption in real life, but it was never actually stated in the scenario. What if *"Did you feel you had a good interview?"* is an interview question which is used to narrow down who to include in the second 50%? – nmclean Feb 10 '14 at 14:33
  • Correct! Not all that participated in these interviews were my friends! – broc.seib Feb 10 '14 at 20:19
  • 2
    "The other two statements are just observations." -- What do you mean "just observations"? Observations hold predictive power. – ahwillia Feb 10 '14 at 21:06
  • 1
    No, feeling you had a good interview does not increase the chances of a second interview; but having a good interview increases both the chance of having a second interview and the chance you'll think you had a good interview. Or, if A increases the odds of B and C, a high result in C probably indicates a high result in B. People's opinions can be unrelated to reality, but according to the evidence in the question itself, that's not the case here. – Ask About Monica Feb 10 '14 at 22:12
  • @AlexWilliams By observation I mean an event that has no bearing on the final outcome. Think of it this way. A person can change there mind as the whether or not they thought they had a good interview but this change of mind in no way could change the outcome and so what you think and what happens are not related. – CeejeeB Feb 11 '14 at 11:51
  • 1
    @CeejeeB Sure, a person's feelings about how an interview went are highly subjective. If we found that whether a person felt he had a good interview turned out to be unrelated to whether he got a second interview, that would not be surprising. And obviously making yourself feel that you had a good interview -- like one of those self-esteem techniques of saying "I had a good interview today" over and over to yourself -- is not going to help. But there's nothing incredible about the theory that people who think that an interview went well may really have had an interview that went well. – Jay Feb 11 '14 at 14:20
  • 2
    Lets say there is a clinical test for some disease that has a false positive rate of 25% and a false negative rate of 5%. Furthermore, lets say that 50% of a population of interest has the disease. If you get a positive test, what are your chances of having the disease? This question is identical in a mathematical sense to the Amazon interview question. Would you still think your chances of having the disease are 50%? – ahwillia Feb 11 '14 at 14:47
  • Feeling is a forecast (from $\hat{f}(t)$) with accuracy $95/(95+75)$. Thus our estimate of $\hat{f}(t)$ is good and we can use it to say that our chance of a second interview is greater than 50%. – Jase Feb 11 '14 at 14:47
  • 50% of all people are female (close enough). If I gave you a complete anatomical description of a person could you honestly say that the odds of them being female was still 50%? I think that any sensible person would give a different answer, based on the description (prior information). – david25272 Feb 11 '14 at 21:38
  • @david25272 that is not quite the same. An Anatomical description would be facts not opinions. If the question was changes to be 95% of all people who answered the interview questions correctly (fact) got a second interview this would be more like your example. Thinking you had a good interview is subjective not fact. – CeejeeB Feb 12 '14 at 07:58
  • 17
    Nobody claims that feeling good about an interview *causes* a second interview to happen. However, it is both plausible and possible for there to be an *association* between that feeling and getting a second interview. (In fact, if we knew how many friends there were we could test the data given in the question for statistical significance.) At the very outset your answer abandons any attempt at exploiting that potentially useful information. That makes it less than a satisfactory response to the question. – whuber Feb 12 '14 at 17:42
  • 2
    This would be true if the question was: *What is the probability that you will have a second interview?*. You could reword it as: *What is the probability that you will have a second interview, given that you felt good or bad about the first?*. But the question that was asked was *What is the probability that you will have a second interview, given that you felt good about the first?*. – nico Feb 13 '14 at 07:27
  • This answer should not be upvoted. – Petter Feb 18 '14 at 10:52
15

The answer that I would give is:

Based on this information, 50%. 'Your friends' is not a representative sample so it should not be considered in the probability calculation.

If you assume that the data is valid then Bayes' theorem is the way to go.

Sam Beckman
  • 151
  • 2
  • 8
    Not a representative sample of what population, exactly? This is not a question about some random interviewee: it's a question about "you." As such it invites us to consider which data are relevant to "you" and to what extent they might be, but your vague use of "representative" just dodges that altogether. – whuber Feb 10 '14 at 15:53
  • @whuber The statistics that were given state that 'your friends' is the sample of the population that is being studied. It strongly implies that population is all the people who have had an interview at Amazon. The statistic (of the sample) is being inferred to discover a parameter (of the population). Then the parameter is applied to an individual of the population as a probability. In this case, the sample is a convenience sample and therefore doesn't represent to population. The question is about probability so it is not about "you," it is about the population, of which you are a member. – Sam Beckman Feb 11 '14 at 03:20
  • What do you mean "not considered"? Where are you drawing this conclusion from? – Jase Feb 11 '14 at 14:48
  • @Jase I mean that the parameter will not be valid if it is based on a non-representative sample. If you include the statistics that are based on a bad sample in your probability calculation, the result will be invalid. This is fundamental to statistics. A sample cannot be assumed to be representative of a population unless that sample has been chosen in a random manner. 'Your friends' is not a random selection so statistics that are derived from that sample shouldn't be used to infer charistics of the population. – Sam Beckman Feb 12 '14 at 08:02
9
  1. State that none of your friends are also up for interview.
  2. State that the question is underconstrained.

Before they can scramble for some further constraint to the problem quickly try and get in a more productive pre-prepared question of your own in a manner fully expecting a response. Maybe you can get them to move on to a more productive interview.

Paddy3118
  • 207
  • 1
  • 3
  • 3
    Why the downvote? An interview is two-way. You need to make sure that this job and these people are a fit for you too. – Paddy3118 Feb 10 '14 at 07:42
  • I like the cheekiness, probably won't get you through, but an amusing approach. – hd1 Feb 10 '14 at 07:42
  • 1
    I don't think stating that none of your friends are up for an interview is a valid answer, nor is it helpful. – gerrit Feb 10 '14 at 10:03
  • 3
    @gerrit, if the job had a component where the applicant had to interpret customer specifications for example, then pointing out that flaw might be the right answer that the interviewer probably didn't hope to receive. – Paddy3118 Feb 10 '14 at 13:10
8

Joke answers but should work well:

  1. "100% When it comes to demanding superb performance from myself, I don't attribute the outcome to any probability. See you in the 2nd interview."
  2. "50%, until my friends got their own Amazon Prime account I won't consider their feelings valid. Actually, sorry, that was a bit too harsh. Let me take it back and rephrase: I won't even consider them human beings."
  3. "Wait, no one ever made my whiny friends feel good. What are your secrets? I want to work for Amazon; give me a chance to please to unpleasable!"
  4. Fake a phone vibration "Oh, sorry! It was just my Amazon Prime account telling me that the Honda I ordered was shipped. Where were we?"
  5. "Regardless, I still feel you should send those who didn't get a 2nd interview a 1-month free trial of Amazon Prime. No one should live their life without knowing its glory. And once we got them, retention, retention, retention."
  6. "55.9% All my friends have an Amazon Prime account and I will make sure to make their experience counts."
Penguin_Knight
  • 11,078
  • 29
  • 48
3

Simple case :

95 / (95 + 75) ≈ 0.559 is a quick way to get to the result Out of people who felt good - 95 succeeded , 75 failed . So thats probability of you passing from that group is above . But

  1. No where it is said you are part of the above group .
  2. If you can think that distributions (your friends circle's) pattern is generic or you are in that group you might as well compute this way
  3. Also IMO not that it matters much but the facts about your friend feelings NEED not have any implication in future - that way its worded . For example it rained yday doesn't mean there is a possibility of rain tommorow unless

Facts , like 50% clearing is not affecting the probability of "what you feel" and the "chances of getting based on that" in that case.

Safer Approach :

However I even would have thought of the 50% thingy above . I.e from the perspective of real facts - 50% is probability makes sense . 1) No where does it say your feelings SHOULD have anything to do with your results .2) There could be ppl who are your friends - but HAD NO feelings - what happened to them ... So given all the combinations that are possible - stick with the safest choice !

PS: I might have flunked this test too.

Nishant
  • 131
  • 4
2

I think the answer is 50% - right at the beginning of the question. It's irrelevant what percentage of your friends feel.

Dmitri
  • 137
  • 2
  • 1
    No. It's not irrelevant. In fact, they tell you explicitly in the question that it's relevant. To make that statement is to completely ignore information in the question and ensure that you will NOT get the job. It's 50% if you assume that none of your friends interviewed, because it's not representative of the actual interviewees. The more friends you have that interviewed, the closer you come to the accepted answer. The less friends you have that interviewed the closer you come to 50%. – Cruncher Feb 11 '14 at 15:02
  • How can you take into account the "Feeling" about the outcome? Let's pretend that of those who did not get the interview 95% thought they did good and of those who got the interview 95% also thought they did good. You see, we changed the "Feeling" percentages but the outcome is still 50/50 – Dmitri Feb 11 '14 at 20:43
  • That is astronomically wrong. In this case it is now 50/50 as you have shown that the "feeling" is irrelevant. As the feeling that they had, had no bearing on the outcome. This is categorically different than the question which shows that the feeling did make a difference. – Cruncher Feb 11 '14 at 20:47
  • Statistics is all about using given information, and forming probabilities with it. You can't just disregard information because it sounds like it shouldn't matter to you. If it said: "95% of the white people got a second interview" and "75% of the people who did not get a second interview were black". Would you ignore this fact and say it's irrelevant if I'm black or white? Or would you statistically consider it? – Cruncher Feb 11 '14 at 20:52
2

The answer is 50%. They told you in the first line what the chance of anyone getting a second interview is. It's a test of your ability to see the essential information and not get distracted by irrelevant noise like how your friends felt. How they felt made no difference.

Thomas Worthington
  • 29
  • 1
  • 3
    If we added the statistic that only 0.00001% of the world's population receive Interview Two, you could use this same logic to say that the probability is always 0.00001%. Obviously, additional factors (such as receiving Interview One) can have an impact on the probability on receiving Interview Two, and we don't know whether how they felt is one of those factors or not. See my comment [here](http://stats.stackexchange.com/a/86039/39859). – nmclean Feb 10 '14 at 15:13
  • 1
    That's wrong. Conditions change the probabilities. I don't have 50% chance to get to the second interview, because I didn't go to the first. What's the chance of you being killed by a car? Is it the same when you're inside your house. What is your chance of being killed in a gas explosion? Is it the same when you feel the smell of gas? – Ark-kun Feb 11 '14 at 13:38
2

Both statements say:

% of your friends

not

% of your friends who were interviewed

We do know that the group "that got a second interview" can only include those who had a first interview. However, the group "that did not get a second interview" includes all other friends.

Without knowing what percentage of your friends were interviewed, it is impossible to identify any correlation between feeling you had a good first interview and receiving a second.

nmclean
  • 121
  • 2
  • 1
    Wrong. The second group did not feel they had a first good interview. Hence, they had it. – Mikaël Mayer Feb 10 '14 at 15:59
  • 1
    @MikaëlMayer Nonsense. Having had the interview is **not** a prerequisite for that statement. NOT having a specific opinion about something includes NOT having ANY opinion about it at all. – nmclean Feb 10 '14 at 16:49
  • 3
    This seems like semantic nitpicking that intentionally avoids using what is clearly the intended interpretation of the question. – Kyle Strand Feb 10 '14 at 19:39
  • 1
    @KyleStrand In the real world, errors in interpreting statistics like this can happen. What you call nitpicking, I call diligence. I would not hesitate to give this answer in the actual interview. First, we don't know that this *wasn't* a deliberate trick of the question. Second, it's not an avoidance as the discussion doesn't need to end there. Once the variables are confirmed, the "expected" answer can be given, but the attention to detail will still be remembered. – nmclean Feb 10 '14 at 20:26
  • I wouldn't hesitate to ask for clarification, but since it seems more likely that the interview question is (in this particular regard) unintentionally vague than that it's intentionally designed to trip you up over this point, I don't think it makes sense to just give this answer and leave it at that; yes, the interviewer may say "good point, let's assume that we meant the percentage of friends interviewed," or they may simply think you're being too anal and difficult to work with and move on to the next question. – Kyle Strand Feb 10 '14 at 20:52
  • I just reread the question, and there's not actually any ambiguity. Both groups of friends **did** feel that they had a good first interview. Thus, even though the second group is given as "your friends that DID NOT get a second interview," if you assume that friends who didn't have an interview at all are included in this group, then you're also assuming that Amazon thinks your friends who didn't even have a first interview are delusional enough to think that they did. This is absurd. – Kyle Strand Feb 10 '14 at 23:03
  • .....unless you're trying to say that the 25% of those who did not get a second interview **and** did not feel that they had a first good interview includes all of the people who did not interview at all, which is not logically absurd but is a pretty bizarre mental leap made solely in order to avoid answering the question as asked. – Kyle Strand Feb 10 '14 at 23:05
  • The fact is that it is obvious to both the interviewer and the interviewee that only statistics about those who **actually had a first interview** are relevant, and therefore, by the principle of relevance, it should be assumed that the interviewer is only talking about those friends. – Kyle Strand Feb 10 '14 at 23:07
  • @KyleStrand No, the second group is **not** constrained to those who felt they had a good first interview. You can call that a "bizarre mental leap" all you want, but recognizing this fact is exactly the type of logical reasoning skills that such a question is designed to gauge. – nmclean Feb 10 '14 at 23:49
  • It seems to me that you're making rather dangerous assumptions about the intent of the question and the attitude of the interviewer. If you ever design an interview question in the way you suggest, I think you'll miss valuable candidates, and if you ever encounter a question like this, I think it's as equally probable that you'll annoy your interviewers as it is that you'll impress them. – Kyle Strand Feb 11 '14 at 01:04
  • Of course, those are only my opinions, and I'm not denying that you're correct to observe that the question technically isn't specified "correctly," in the sense that the implied meaning isn't precisely equivalent to the set-theoretical meaning as currently worded. (I say "implied meaning" because I'm sure you'd agree that in normal English, "my friend Jo didn't get a second interview" usually means that Jo **did** get a first interview.) – Kyle Strand Feb 11 '14 at 01:05
  • 2
    @KyleStrand You're suggesting that someone would ignore my request for more relevant data because they find it annoying. Sorry, but interviews are two-way, and you're describing an interviewer with a very unprofessional attitude. If someone becomes annoyed and dismissive at the prospect of critical analysis *while interviewing for a job that calls for critical analysis*, don't expect me to stick around. – nmclean Feb 11 '14 at 05:36
  • I didn't actually suggest that; in fact, I said "I wouldn't hesitate to ask for clarification, but...I don't think it makes sense to just give this answer and leave it at that." – Kyle Strand Feb 11 '14 at 16:44
  • @KyleStrand Your critical mistake was in assuming that the answer is intended as an *avoidance* tactic, which I immediately corrected in my first reply, which you evidently ignored so you could continue attacking that strawman. Again, the point is to draw attention to the missing information; the discussion does **not** end there. – nmclean Feb 11 '14 at 17:18
  • Well, I guess just to complete the circle I'll quote the second half of the comment I just quoted: 'yes, the interviewer may say "good point, let's assume that we meant the percentage of friends interviewed," or they may simply think you're being too anal and difficult to work with and move on to the next question.' I should probably be more charitable and assume that you wouldn't *let* the conversation end there, but your initial attitude struck me as more combative than logically conscientious. – Kyle Strand Feb 11 '14 at 17:43
  • @KyleStrand The second half of that comment is exactly what I was referring to. Moving on to the next question without addressing the criticism is dismissive, rude, and would lead me to believe that the person is reciting questions without an understanding of their significance and is poorly suited to evaluating employees for analytical skill. – nmclean Feb 11 '14 at 18:20
2

This being an interview question, I don't believe there is a correct answer. I would most likely calculate the ~56% using Bayes and then tell the interviewer:

Without any knowledge about me, it could be between 50% and 56%, but because I know me and my past, the probability is 100%

Josef says Reinstate Monica
  • 131
  • 5
1

It might be helpful to view this chain of events as a binary tree where just two leaf probabilities are relevant. The root node contains all folks who had a 1st interview; we then split this group on being invited to a 2nd interview ("2nd", "no 2nd") and subsequently on whether they felt good about the 1st interview ("good", "bad"). The conditional probabilities $P(\text{good} | \text{2nd}) = 0.95$ and $P(\text{good} | \text{no 2nd}) = 0.75$ are positioned at the edges.

For educational reasons, we present two versions: one with decimal probabilities and the other with absolute counts -assuming a population of $200$.

enter image description here

We can now directly compute the conditional probability (of receiving a second interview given that you had a good first interview) from the leaf probabilities in two ways:

$$ P(\text{2nd } | \text{ good}) = \frac{P(\text{2nd} \cap \text{good})}{P( \text{good})} = \frac{0.475}{0.475 + 0.375} = \frac{95}{95 + 75} \approx 0.56 $$

Markus Loecher
  • 788
  • 3
  • 11
1

Mathematically

You're chances are 50%. This is because in the Venn diagram of Amazon Interviewees you fall into the Universal Set of ALL Interviewees, but not the set of 'Your friends'.

enter image description here

Had the question stated: 'One of your friends had a great interview. What is the percentage she'll get a second interview?' Then the current top answer would be valid. But those 2nd and 3rd statistics only apply to you if you consider yourself one of your own friends. So, maybe it's more of a psychological question?

MDMoore313
  • 127
  • 4
  • 1
    Presenting this as an interview question has caused people to imagine that there are all sorts of semantic minefields. You could certainly preface your answer with "Assuming I'm like my friends....", but I doubt the interviewer would let you off the hook with this answer. – Matt Krause Feb 10 '14 at 16:02
  • 4
    This would have been the obvious answer if it hadn't been stated that you thought you had a good interview. That's extra information. You fall in the part of the Venn diagram of all Amazon interviewees that thought they had a good interview, which is of unknown size, but can maybe be estimated somewhat. – RemcoGerlich Feb 10 '14 at 17:19
  • @RemcoGerlich Estimated how? based on friends? – MDMoore313 Feb 10 '14 at 17:42
  • 1
    Well, it's not perfect, but it's better than nothing, isn't it? – RemcoGerlich Feb 10 '14 at 17:57
  • 1
    @RemcoGerlich lol that's debatable :-) – MDMoore313 Feb 10 '14 at 20:20
  • 1
    -1 if I could, this is so wrong. You don't *actually* belong to either set, since in both cases the samples exclude you (the *all candidates* sample doesn't include you, it simply includes all candidates in the past before you). Further, intuitively it seems to be the case that you might be more similar to your friends than to the average member of the general sample, and thus you might be more likely to fall in line with the likelihood of your friends because of this. – Muhd Feb 11 '14 at 01:38
  • Why not draw the "people, who feel good about their interview" set? – Ark-kun Feb 11 '14 at 13:32
  • @Muhd, do both cases you mention are possible, but assumptions. We have no information given to confirm this. My answer is based solely on information given. The question does not state `50% of ALL candidates in have past have had....` In the case of statement 1 Amazon is basically guaranteeing that if they Interview 2 people, 1 person will receive a second interview. Also, the only scientific data you will *ever* have will be historical data, unless you find a way to look into the future. – MDMoore313 Feb 11 '14 at 13:39
  • @Ark-kun you could, but you don't have any data about that set besides the fact that *some* of your friends fall into it, and some don't. – MDMoore313 Feb 11 '14 at 13:40
  • You say that there is zero in common between the person and the sample of his friends. Others imply that the person and his friends are a sample of a homogenous set. Aren't you both making strong assumptions in the absence of data? Isn't your 50% as wrong as 56% ? – Ark-kun Feb 11 '14 at 14:21
  • 2
    You really think it's 50%? If I gave you 2 interviewees. And I said, one of them thought they had a really good interview, and the other thought they blew it. Do you think it's a 50/50 chance who got the second interview? Of course not, and you'd be a bozo to think to so. Apart from that, the question EXPLICITLY tells you, that more people that thought they had a good interview, get a second one. – Cruncher Feb 11 '14 at 15:00
  • 1
    A big part of Amazon's business model is inferring similarities between people based on graph networks. Explicitly rejecting the hypothesis that you have something in common with your friends runs counter to this intuition. Context here is important, I think. – david25272 Feb 11 '14 at 21:49
  • @Cruncher The question also states that there are people who thought they did bad that got a second interview as well, which validates my point: How they felt is irrelevant. I've seen people who thought they bombed a test only to get a great grade, and I've seen the same with interviews. How does what an interviewee feel after the interview have any bearing on an orgs decision to hire them? It doesn't. Amazon is merely presenting facts in statement #1, and giving you statistics about your friends in statements 2 and 3, trying to draw your attention away from the facts, classic test strategy. – MDMoore313 Feb 13 '14 at 16:51
  • @david25272 You say I'm rejecting it, I'm saying I've considered it and determined those facts don't hold weight in answering the question @ hand. – MDMoore313 Feb 13 '14 at 16:55
  • @MDMoore313 Ah but 75% < 95% indicating that feeling good about the interview does have impact. If the 2 numbers were identical you can conclude irrelevance. It's not that "their feeling changes the interviewers mind". It's if they ACTUALLY did good, they have a higher chance of THINKING they did good. If I say 95% of people that run regularly have strong legs. Then I give you 2 people. One with strong legs and one with weak legs. Which will you think is the runner? – Cruncher Feb 13 '14 at 16:56
  • @Ark-kun I'm not saying there is zero in common. Looking at the diagram I've added we can see one thing they surely have in common is that they've all interviewed with Amazon, that is given and no assumption was made about that. My 50% could be wrong, but where I differed is that I didn't assume any data in my calculation that wasn't already present. – MDMoore313 Feb 13 '14 at 16:57
  • @MDMoore313 by stating 50% you are actually assuming that none of your friends interviewed. So yes you are assuming some data. – Cruncher Feb 13 '14 at 16:58
  • @Cruncher and everyone else I'd be glad to continue this in the chat, as the comment section is for Q/A clarification. – MDMoore313 Feb 13 '14 at 17:00
  • @MDMoore313 You're basically saying that the interviewee interview impression provides zero information about the result (does not reduce the entropy of the result). Let's test it empirically. We take 1000 people who were interviewed at Amazon and felt that they did good on the first interview. If they had the 2nd interview, you pay me `$1`. Otherwise I pay you `$1`. – Ark-kun Feb 14 '14 at 02:38
0

Answer is: ≈1

The question doesnt provide how many people among those appearing for interview,are our friends.However, we can assume that data & get any answer we want.Also, main thing about this assumption is that only our friends get selected for 2nd interview.

Lets say 104 of your friends appear for the interview,& 100 of them get 2nd interview. So, we can say 95 of them felt they had a good first interview(Criteria 2).Also, out of remaining 4,75%(ie 3) of them felt they had a good interview(Criteria 3).So out of 104, 98 felt they had a good interview.but 95 were selected.so final probability is : 95/98.We can always say that 100*2 = 200(104 are friends out of them) people in total gave the first interview, in order to satisfy the 1st criteria.here, all 96 who were not friends,failed to clear 1st interview.

Now you increase friends to 108 & do it again, for 100 of them getting 2nd interview.your final probability would be 101/108 .Thus, as we increase no of friends who didnt clear first interview, the probability decreases.So for maximum efficiency, no of friends who didnt clear should always be 4.

Now increase the friends.Suppose they are 10,004(10000 who cleared,4 who didnt). so now, out of 10000,9500 felt they had a good interview.So in total, 9503(among 4 failed,3 felt they had good interview, therefore 9500+3) felt they had a good interview,but only 9500 cleared. ie final probability = 9500/9503 which is ≈1.Again, we can put that 20000 people in total appeared for the interview, & all those who werent friends, couldnt clear it.So, 1st criteria is again satisfied.

Note: Our assumption about no of friends,no of them clearing the interview & no of other participants, is all in order to get the probability to 1.we can modify this data & can get any probability we want.

Sumedh
  • 109
  • 3