Sampling distribution of the radius of 2D normal distribution

Question

The bivariate normal distribution with mean $\mu$ and covariance matrix $\Sigma$ can be re-written in polar coordinates with radius $r$ and angle $\theta$. My question is: What is the sampling distribution of $\hat{r}$, that is, of the distance from a point $x$ to the estimated center $\bar{x}$ given the sample covariance matrix $S$?

Background: The true distance $r$ from a point $x$ to mean $\mu$ follows a Hoyt distribution. With eigenvalues $\lambda_{1}, \lambda_{2}$ of $\Sigma$, and $\lambda_{1} > \lambda_{2}$, its shape parameter is $q=\frac{1}{\sqrt{(\lambda_{1}+\lambda_{2})/\lambda_{2})-1}}$, and its scale parameter is $\omega = \lambda_{1} + \lambda_{2}$. The cumulative distribution function is known to be the symmetric difference between two Marcum Q-functions.

Simulation suggests that plugging in estimates $\bar{x}$ and $S$ for $\mu$ and $\Sigma$ into the true cdf works for large samples, but not for small samples. The following diagram shows the results from 200 times

• simulating 20 2D normal vectors for each combination of given $q$ ($x$-axis), $\omega$ (rows), and quantile (columns)
• for each sample, calculating the given quantile of the observed radius $\hat{r}$ to $\bar{x}$
• for each sample, calculating the quantile from the theoretical Hoyt (2D normal) cdf, and from the theoretical Rayleigh cdf after plugging in the sample estimates $\bar{x}$ and $S$.

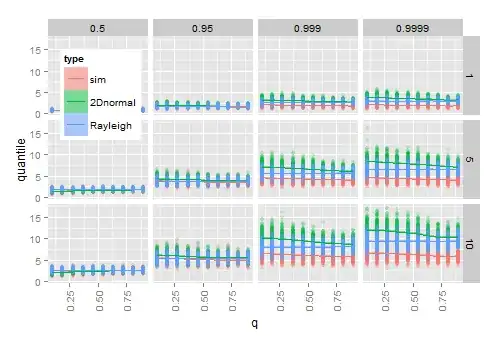
As $q$ approaches 1 (the distribution becomes circular), the estimated Hoyt quantiles approach the estimated Rayleigh quantiles which are unaffected by $q$. As $\omega$ grows, the difference between the empirical quantiles and the estimated ones increases, notably in the tail of the distribution.

Answer 1

As you mentioned in your post we know the distribution of the estimate of $\widehat{r_{true}}$ if we are given $\mu$ so we know the distribution of the estimate $\widehat{r^2_{true}}$ of the true $r^2$.

We want to find the distribution of $$\widehat{r^2} = \frac{1}{N}\sum_{i=1}^N (x_i-\overline{x})^T(x_i-\overline{x})$$ where $x_i$ are expressed as column vectors.

We now do the standard trick

$$\begin{eqnarray*} \widehat{r^2_{true}} &=& \frac{1}{N}\sum_{i=1}^N(x_i - \mu)^T(x_i-\mu)\\ &=& \frac{1}{N}\sum_{i=1}^N(x_i-\overline{x} + \overline{x} -\mu)^T(x_i-\overline{x} + \overline{x}-\mu)\\ &=&\left[\frac{1}{N}\sum_{i=1}^N(x_i - \overline{x})^T(x_i-\overline{x})\right] + (\overline{x} - \mu)^T(\overline{x}-\mu) \hspace{20pt}(1)\\ &=& \widehat{r^2} + (\overline{x}-\mu)^T(\overline{x}-\mu) \end{eqnarray*} $$ where $(1)$ arises from the equation $$\frac{1}{N}\sum_{i=1}^N(x_i-\overline{x})^T(\overline{x}-\mu) = (\overline{x} - \overline{x})^T(\overline{x} - \mu) = 0$$ and its transpose.

Notice that $\widehat{r^2}$ is the trace of the sample covariance matrix $S$ and $(\overline{x}-\mu)^T(\overline{x}-\mu)$ only depends only on the sample mean $\overline{x}$. Thus we have written $$\widehat{r_{true}^2} = \widehat{r^2} + (\overline{x}-\mu)^T(\overline{x}-\mu)$$ as the sum of two independent random variables. We know the distributions of the $\widehat{r^2_{true}}$ and $(\overline{x} - \mu)^T(\overline{x}-\mu)$ and so we are done via the standard trick using that characteristic functions are multiplicative.

Edited to add:

$||x_i-\mu||$ is Hoyt so it has pdf $$f(\rho) = \frac{1+q^2}{q\omega}\rho e^{-\frac{(1+q^2)^2}{4q^2\omega} \rho^2}I_O\left(\frac{1-q^4}{4q^2\omega} \rho^2\right)$$ where $I_0$ is the $0^{th}$ modified Bessel function of the first kind.

This means that the pdf of $||x_i-\mu||^2$ is $$f(\rho) = \frac{1}{2}\frac{1+q^2}{q\omega}e^{-\frac{(1+q^2)^2}{4q^2\omega}\rho}I_0\left(\frac{1-q^4}{4q^2\omega}\rho\right).$$

To ease notation set $a = \frac{1-q^4}{4q^2\omega}$, $b=-\frac{(1+q^2)^2}{4q^2\omega}$ and $c=\frac{1}{2}\frac{1+q^2}{q\omega}$.

The moment generating function of $||x_i-\mu||^2$ is $$\begin{cases} \frac{c}{\sqrt{(s-b)^2-a^2}} & (s-b) > a\\ 0 & \text{ else}\\ \end{cases}$$

Thus the moment generating function of $\widehat{r^2_{true}}$ is $$\begin{cases} \frac{c^N}{((s/N-b)^2-a^2)^{N/2}} & (s/N-b) > a\\ 0 & \text{else} \end{cases}$$ and the moment generating function of $||\overline{x} - \mu||^2$ is $$\begin{cases} \frac{Nc}{\sqrt{(s-Nb)^2-(Na)^2}} = \frac{c}{\sqrt{(s/N-b)^2-a^2}} & (s/N-b) > a\\ 0 & \text{ else} \end{cases}$$

This implies that the moment generating function of $\widehat{r^2}$ is $$\begin{cases} \frac{c^{N-1}}{((s/N-b)^2-a^2)^{(N-1)/2}} & (s/N-b) > a\\ 0 & \text{ else}. \end{cases}$$

Applying the inverse Laplace transform gives that $\widehat{r^2}$ has pdf $$g(\rho) = \frac{\sqrt{\pi}Nc^{N-1}}{\Gamma(\frac{N-1}{2})}\left(\frac{2\mathrm{i} a}{N\rho}\right)^{(2 - N)/2} e^{b N \rho} J_{N/2-1}( \mathrm{i} a N \rho).$$