31

I'm performing an elastic-net logistic regression on a health care dataset using the glmnet package in R by selecting lambda values over a grid of $\alpha$ from 0 to 1. My abbreviated code is below:

alphalist <- seq(0,1,by=0.1)
elasticnet <- lapply(alphalist, function(a){
  cv.glmnet(x, y, alpha=a, family="binomial", lambda.min.ratio=.001)
})
for (i in 1:11) {print(min(elasticnet[[i]]$cvm))}

which outputs the mean cross validated error for each value of alpha from $0.0$ to $1.0$ with an increment of $0.1$:

[1] 0.2080167
[1] 0.1947478
[1] 0.1949832
[1] 0.1946211
[1] 0.1947906
[1] 0.1953286
[1] 0.194827
[1] 0.1944735
[1] 0.1942612
[1] 0.1944079
[1] 0.1948874

Based on what I've read in the literature, the optimal choice of $\alpha$ is where the cv error is minimized. But there's a lot of variation in the errors over the range of alphas. I'm seeing several local minimums, with a global minimum error of 0.1942612 for alpha=0.8.

Is it safe to go with alpha=0.8? Or, given the variation, should I re-run cv.glmnet with more cross validation folds (e.g. $20$ instead of $10$) or perhaps a larger number of $\alpha$ increments between alpha=0.0 and 1.0 to get a clear picture of the cv error path?

MichaelChirico
  • 1,270
  • 1
  • 9
  • 20
RobertF
  • 4,380
  • 6
  • 29
  • 46
  • 7
    You would want to take a look at `caret` package which can do repeated cv and tune for both alpha & lambda(supports multicore processing!). From memory, I think the `glmnet` documentation advices against tuning for alpha the way you doing here. It recommends to keep the foldids fixed if the user is tuning for alpha in addition to the tuning for lambda provided by `cv.glmnet`. –  Jan 31 '14 at 17:21
  • Thanks, I'll look at caret. I see the glmnet documentation recommends calling cv.glmnet with a precomputed vector foldid (p. 4). If I stick with the glmnet package, do I need to randomly assign my dataset records to foldids of 1 thru 10, then invoke elasticnet ten times: elasticnet.f – RobertF Jan 31 '14 at 17:45
  • 1
    Ah, found this post here: http://stats.stackexchange.com/questions/69638/does-caret-train-function-for-glmnet-cross-validate-for-both-alpha-and-lambda?rq=1 – RobertF Jan 31 '14 at 18:30
  • 2
    don't forget to fix the foldid when you are trying different $\alpha$ – Areza Dec 07 '15 at 14:03
  • 1
    For reproducibility, never run `cv.glmnet()` without passing in `foldids` created from a known random-seed. – smci Feb 24 '17 at 01:24
  • This question has an accepted answer that is downvoted and crossed out because its author agreed the answer was wrong. Don't you want to de-accept it?? Simply click on the green tick to remove the "acceptance" mark. – amoeba Feb 22 '18 at 08:46
  • 1
    @amoeba have a look at my answer - input on the trade-offs between l1 and l2 are welcome ! – Xavier Bourret Sicotte Nov 03 '18 at 17:45

2 Answers2

11

Clarifying what is meant by $\alpha$ and Elastic Net parameters

Different terminology and parameters are used by different packages, but the meaning is generally the same:

The R package Glmnet uses the following definition

$\min_{\beta_0,\beta} \frac{1}{N} \sum_{i=1}^{N} w_i l(y_i,\beta_0+\beta^T x_i) + \lambda\left[(1-\alpha)||\beta||_2^2/2 + \alpha ||\beta||_1\right]$

Sklearn uses

$\min_{w} \frac{1}{2N} \sum_{i=1}^{N} ||y - Xw ||^2_2 + \alpha \times l_1 \text{ratio} ||w||_1 + 0.5 \times \alpha \times (1 - l_1 \text{ratio}) \times ||w||_2^2$

There are alternative parametrizations using $a$ and $b$ as well..

To avoid confusion i am going to call

  • $\lambda$ the penalty strength parameter
  • $L_1 \text{ratio}$ the ratio between $L_1$ and $L_2$ penalty, ranging from 0 (ridge) to 1 (lasso)

Visualizing the impact of the parameters

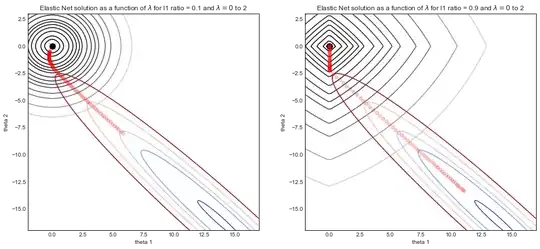
Consider a simulated data set where $y$ consists of a noisy sine curve and $X$ is a two dimensional feature consisting of $X_1 = x$ and $X_2 = x^2$. Due to correlation between $X_1$ and $X_2$ the cost function is a narrow valley.

The graphics below illustrate the solution path of elasticnet regression with two different $L_1$ ratio parameters, as a function of $\lambda$ the strength parameter.

  • For both simulations: when $\lambda = 0$ then the solution is the OLS solution on the bottom right, with the associated valley shaped cost function.
  • As $\lambda$ increases, the regularization kicks in and the solution tends to $(0,0)$
  • The main difference between the two simulations is the $L_1$ ratio parameter.
  • LHS: for small $L_1$ ratio, the regularized cost function looks a lot like Ridge regression with round contours.
  • RHS: for large $L_1$ ratio, the cost function looks a lot like Lasso regression with the typical diamond shape contours.
  • For intermediate $L_1$ ratio (not shown) the cost function is a mix of the two

enter image description here

Understanding the effect of the parameters

The ElasticNet was introduced to counter some of the limitations of the Lasso which are:

  • If there are more variables $p$ than data points $n$, $p>n$, the lasso selects at most $n$ variables.
  • Lasso fails to perform grouped selection, especially in the presence of correlated variables. It will tend to select one variable from a group and ignore the others

By combining an $L_1$ and a quadratic $L_2$ penalty we get the advantages of both:

  • $L_1$ generates a sparse model
  • $L_2$ removes the limitation on the number of selected variables, encourages grouping and stabilizes the $L_1$ regularization path.

You can see this visually on the diagram above, the singularities at the vertices encourage sparsity, while the strict convex edges encourage grouping.

Here is a visualization taken from Hastie (the inventor of ElasticNet)

enter image description here

Further reading

Xavier Bourret Sicotte
  • 7,986
  • 3
  • 40
  • 72
5

Let me add some very practical remarks despite the age of the question. As I am not a R user, I cannot let code talk, but it should be understandable nevertheless.

  1. Normally you should just pick the hyperparameters (here: $\alpha$) with the best CV score. Alternatively, you could select the best $k$ models $f_1, ..., f_k$ and form an ensemble $f(x) = \frac{1}{k}\sum_i{f_i(x)}$ by arithmetic averaging the decision function. This, of course, gives you an increase of runtime complexity. Hint: sometimes geometric averaging works better $f(x) = \sqrt[k]{\prod_{i=1}^k{f_i(x)}}$. I suppose this is because of a smoother resulting decision boundary.

  2. One advantage of resampling is that you can inspect the sequence of test scores, which here are the scores of the cv. You should always not only look at the average but at the std deviation (it is not normal distributed, but you act as if). Usually you display this say as 65.5% (± 2.57%) for accuracy. This way you can tell whether the "small deviations" are more likely to be by chance or structurally. Better would be even to inspect the complete sequences. If there is always one fold off for some reason, you may want to rethink the way you are doing your split (it hints a faulty experimental design, also: did you shuffle?). In scikit-learn the GridSearchCV stores details about the fold expirements in cv_results_ (see here).

  3. With regards to the $\alpha$: the higher it is, the more your elastic net will have the $L_1$ sparsity feature. You can check the weights of the resulting models, the higher the $\alpha$ is, the more will be set to zero. It is a useful trick to remove the attributes with weights set to zero from your pipeline all together (this improves runtime performance dramatically). Another trick is to use the elastic net model for feature selection and then retrain a $L_2$ variant. Usually this leads to a dramatic model performance boost as intercorrelations between the features have been filtered out.

uberwach
  • 216
  • 2
  • 3