Using Excel's correlation function I get a correlation of -7% between data sets A & B. Data set C has a 92% correlation to A and an 84% correlation to B. How can C be strongly correlated to A and B, but A and B are slightly negatively correlated to one another?
What other tests can I perform to help me better understand the relationships between A, B & C?
You could make scatter plots of each with each.
As to how it is possible, imagine this:
a and b are entirely independent.
c = a + b.
So, we would have something like (in R code; stuff following a # is comment)
set.seed(1)
a <- rnorm(100)
b <- rnorm(100)
c <- a + b
cor(a,b) # - 0.0009
cor(a,c) # 0.68
cor(b,c) #0.72
Consider this simple path model / directed acyclical graph (DAG):
Here we see that $C$ is caused by both $A$ and $B$, but they are unrelated to each other. This is sometimes called a common effect model, or a collider.
Here is a very simple simulation done with R:
set.seed(1) # this makes the simulation exactly reproducible
A = rnorm(50, mean=0, sd=1) # here I generate data from 2 normal distributions
B = rnorm(50, mean=0, sd=1)
C = A + B + rnorm(50, mean=0, sd=.5) # C is caused by A & B plus some random noise
# here are the correlations amongst these three variables:
cor(A, B) # -0.03908718
cor(A, C) # 0.6016085
cor(B, C) # 0.7006461
This is what the data look like when you make a scatterplot matrix:
Of course, this doesn't have to be causal, that is primarily an intuitional convenience. You could simply have points located in this manner in a three dimensional space. Here is an attempt to picture these points in 3D:
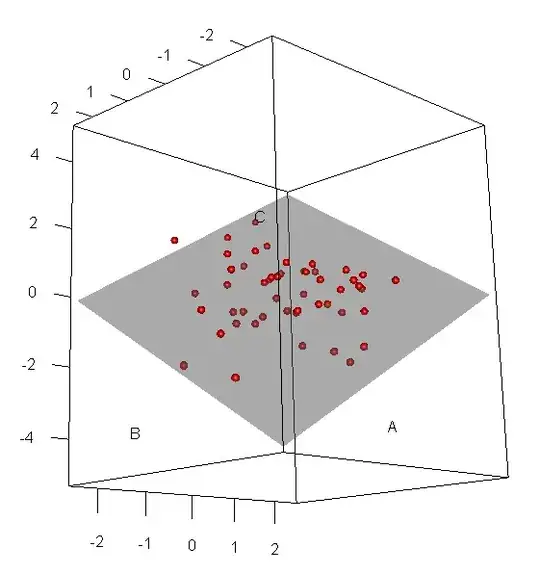
It is possible because it depends on how your data suspend in the 3D space. See this doughnut for an example:
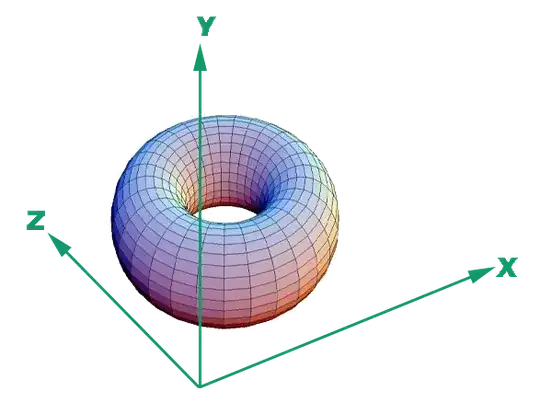
Suppose the doughnut is lying on the floor happily, from the y,z plane and at the x,y plane, the doughnut should look like an oblong shape (you will not see the hole). But when you look at the x,z plane (aka top down bird view), it'd be a circle.
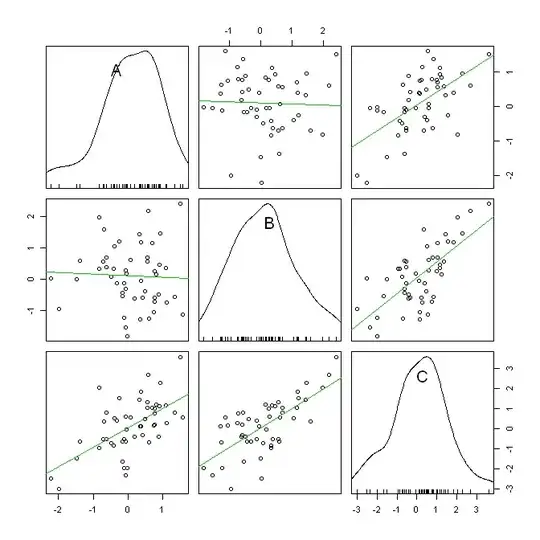
Your case is quite like this, with the far end of the doughnut slightly lifted upward to give the oblong shapes a bit of an angle and a high positive correlation. While when you look at the third pair, you don't see that high positive correlation anymore. Instead, you see a bit of an oval that shows a negative correlation between x and z.
As an extension, you'll find that in order for your expectation to be true, the cloud of data probably should look like a sausage stemming away from the origin. That way, no matter how you rotate the cube, you should still see a strong positive correlation from all the three sides.
As for how to detect, examining all pair-wise scatter plots will help. Interactive 3D plot that allows you to rotate the axes should also let you get a better understanding of the actual dispersion.
I would use "pairs" function in R to check out the scatter matrix, where you see the scatter of any pair of variables. This might help to understand the data better
