Removing parameters in SEM when $\chi^2$ value and DF are 0

Question

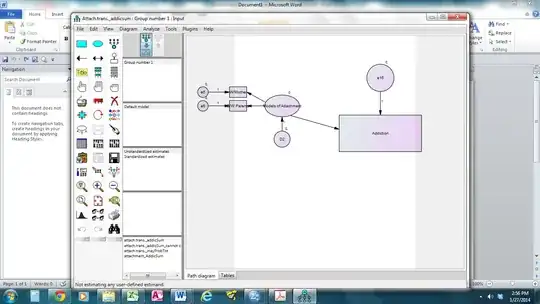
I am VERY new to SEM. I ran a model where I obtained 0 DF, so it could not compute the fit. So, I am left to cut out parameters. HOWEVER, I'm not sure where I can cut them in my particular case. I have attached here a screenshot of my model...you can see there are not too many parameters. I am trying to test to see if Emotional Models of Attachment (measured by early relationships) affect level addiction (measured in the survey).

1. I'm not sure how I can cut down parameters without losing the whole meaning. For example, I can cut out the latent variable, and just look at the data as a path analysis from the early relationship measures to Addiction... but that would eliminate the theory that Attachment Models are involved, right?

2. Also, in researching more about constraining, I read that I can set the regression (number by the arrow) at 1. But in my case, this would sort of ruin the whole point of running my model, correct? When is good practice to constrain from a latent variable?

Thank you!

Answer 1

As the model stands, it is effectively a model with one common factor (Models of Attachment) and three indicators. Such a model is just identified (0 DF) unless there is more to the model. So besides imposing constraints on this model, think about expanding the model to include other variables. You might be headed that way already, in which case the current problem is really not a problem at all.

Currently, all three observed variables are, effectively, indicators of the one common factor, even if you think of Addiction as a "separate" dependent variable. So the common factor is whatever is common to all three observed variables. That may change as you expand the model, but you should keep an eye on it.

Answer 2

Your model is saturated - you are estimating three regression loadings, and you have three covariances (or correlations), so you have zero degrees of freedom. Nothing wrong with testing that hypothesis, if that's the model that you are interested in, but there's no need to use a structural equation model to estimate it - you could have estimated this model using regression.

You need more indicators of your latent variables if you want to ensure that this model is over-identified and not saturated, and therefore has positive df and chi-square.

Answer 3

Practical advice

Your situation is very common, and as @JeremyMiles correctly noted, when your model has df=0, you have perfect model fit. From the picture provided, you set residual variances of both items associated with your latent construct to 1. This is a rather unconventional approach to sem/cfa model identification. I suggest the following:

1. Set the loading of item 1 associated with your latent variable to be 1. This sets the metric for the model.

2. Next, set residual variance of item 2 associated with the latent construct to 1. This introduces a model constraint, so you no longer have df=0.

3. Then re-estimate your model and you should get your model fit statistics.