Generally, the sign test is used to test the hypothesis that the difference median is zero between two continuous distributions (Sign test).
I am trying to understand whether it can be adapted to prove that the values from one distribution are generally lower than the other. Or are there better tests which can be designed for this purpose?
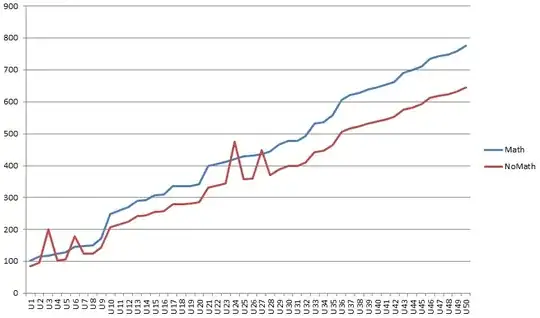
Data available: Suppose that I have the average GMAT scores from 50 universities. There are 2 averages per university, the first one being the average of those candidates who have studied mathematics at a graduate level while the second one is for those who have not.
A simple plot shows that students who have studied math score higher. However, I would like to prove this fact statistically using a test (and a p-value?). Conversely, I may also like to prove in another case that there is no difference.